Question: 6. Let w := e2mi/3 2 Vi in C. (a) Show that the subset Z[w] := {aEC: there exist a, bEZ such that a =
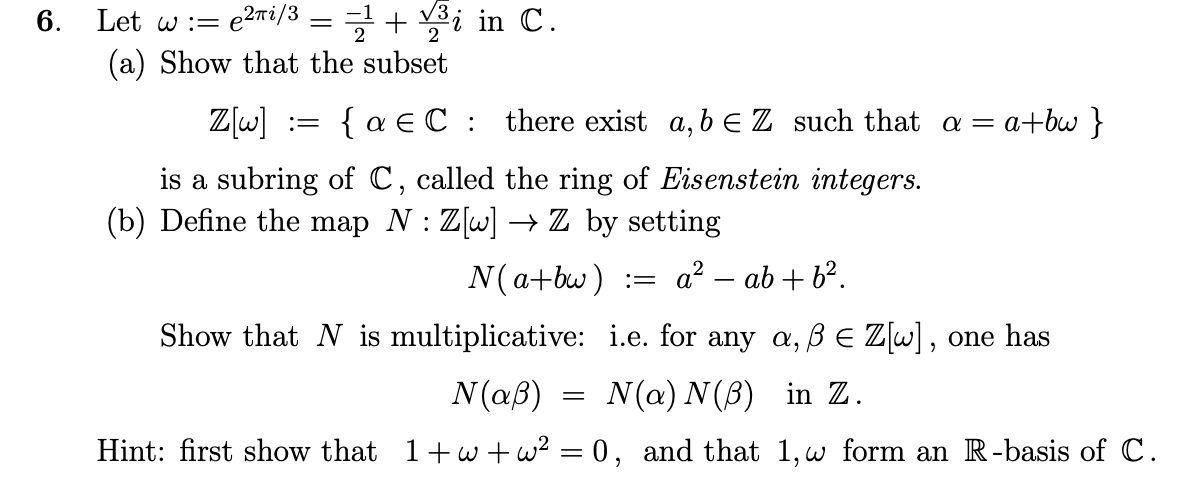
![that the subset Z[w] := {aEC: there exist a, bEZ such that](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/670a6597a4599_615670a659791152.jpg)
6. Let w := e2mi/3 2 Vi in C. (a) Show that the subset Z[w] := {aEC: there exist a, bEZ such that a = atbw} is a subring of C, called the ring of Eisenstein integers. (b) Define the map N : Z[w] - Z by setting N(atbw ) := a2 - ab+ 62 Show that N is multiplicative: i.e. for any a, B E Z[w], one has N(aB) = N(a) N(B) in Z. Hint: first show that 1 +w +w2 =0, and that 1, w form an R-basis of C.8. Keep the notation as in the previous question. Show that Z[w] is a Euclidean domain, by showing that the map N : Z[w] > Z is an Euclidean function for Z[w]
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


