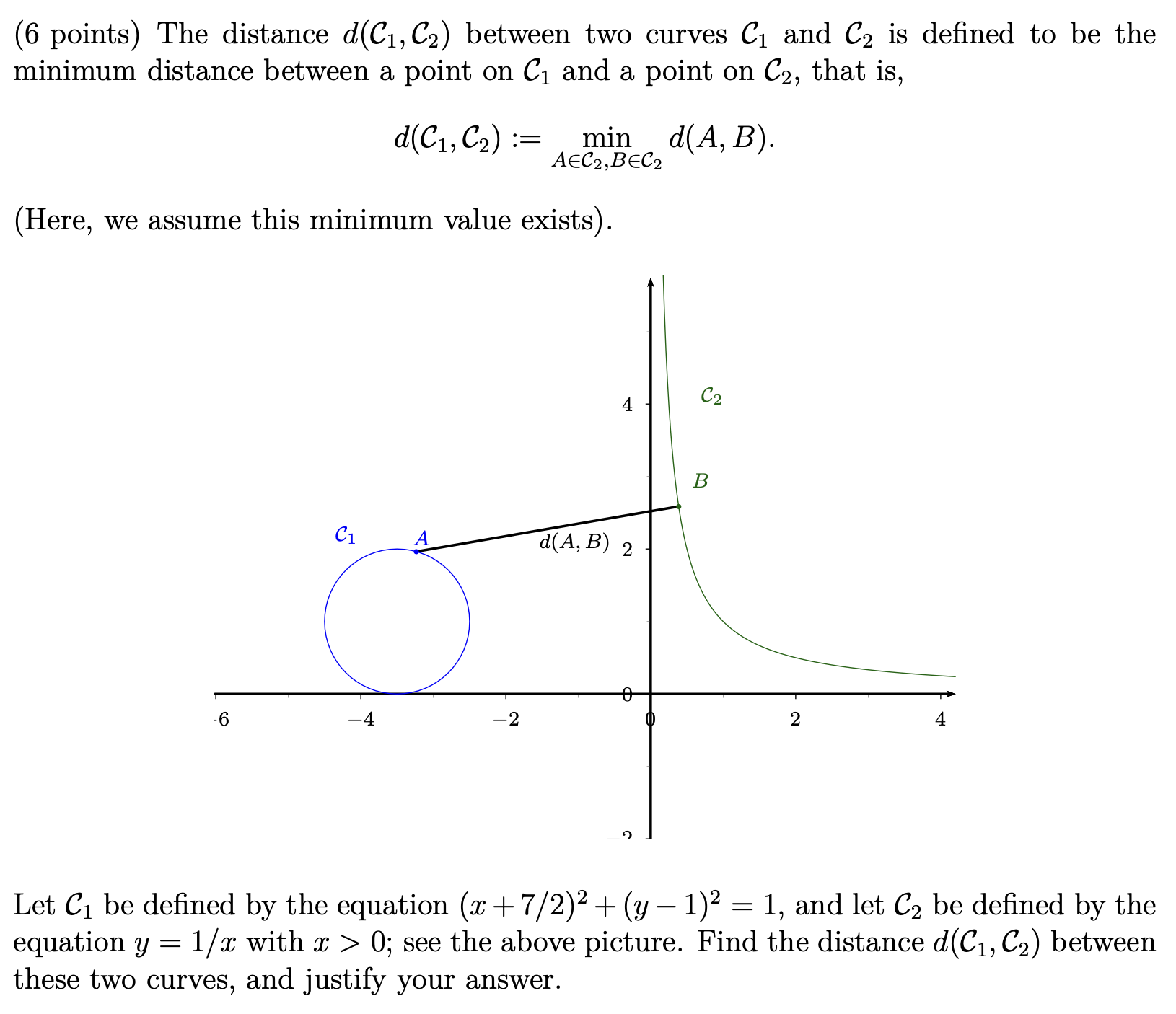
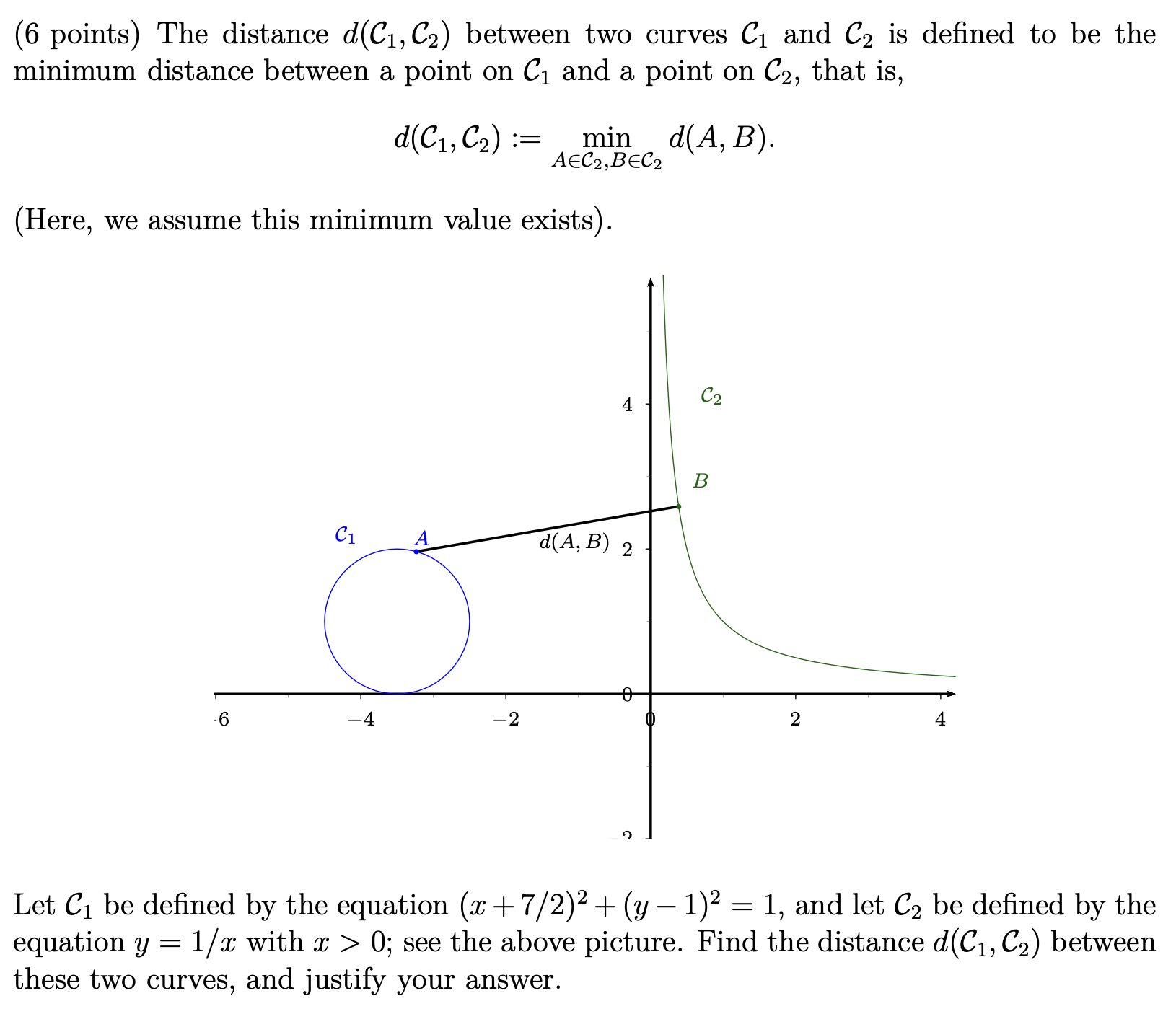
(6 points) The distance d(C1, C2) between two curves C1 and C2 is defined to be the minimum distance between a point on C1 and a point on C2, that is, d(C1, C2) := min d(A, B). AEC2, BEC2 (Here, we assume this minimum value exists). 4 C2 B C1 d( A, B) 2 - 6 -4 -2 2 4 Let C1 be defined by the equation (x + 7/2)2 + (y -1)2 = 1, and let C2 be defined by the equation y = 1/x with x > 0; see the above picture. Find the distance d(C1, C2) between these two curves, and justify your