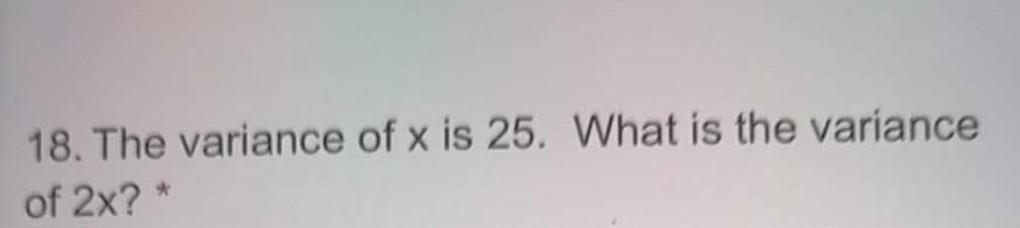
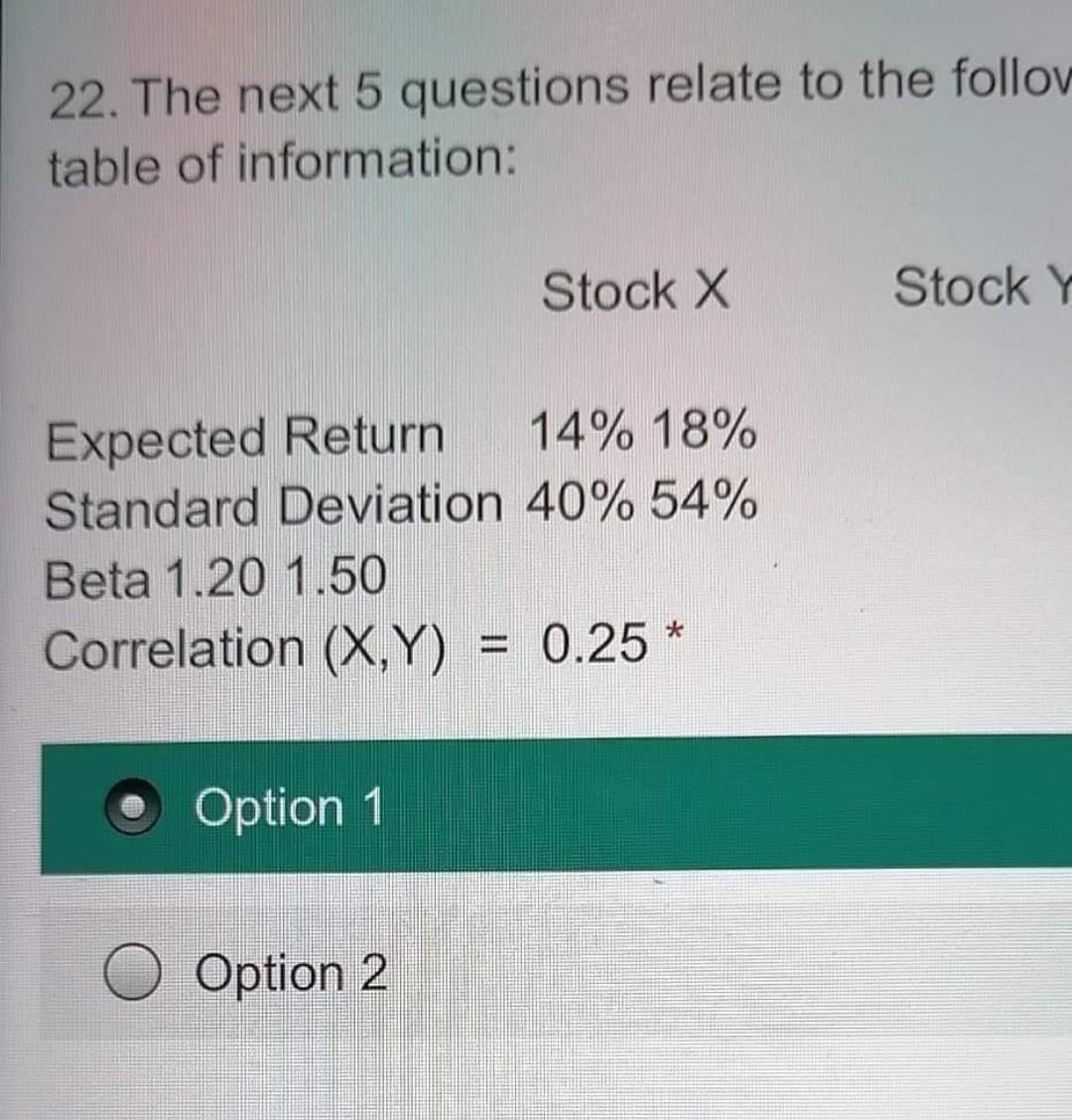
6. Portfolio P consists of 2 assets (b and s). If Er_b)= 5%, o_b=8%, E(r_s)= 10%, o_s=19%, the correlation coefficient is 0.2. Then, answer the following three questions. The E(r_p) and the o_p are equal to and respectively. * 1. Consider the following two stocks, A and B. Stock A has an expected return of 10% and a beta of 1.20. Stock B has an expected return of 14% and a beta of 1.80. The expected market rate of return is 9% and the risk-free rate is 5%. Security would be considered a good buy because 2. Portfolio A has a beta of 0.5 on factor 1 and a beta of 1.25 on factor 2. The risk premiums on the factors 1 and 2 portfolios are 1% and 7% respectively. The risk-free rate of return is 7%. The expected return on portfolio A is arbitrage opportunities exist. * if no 3. The risk-free rate is 4%. The expected market rate of return is 11%. If you expect stock X with a beta of .8 to offer a rate of return of 12 percent, then you should 4.17 = 7%. A well-diversified portfolio (H) has a b H = 1.3 and a H = 2%. A well-diversified portfolio (Z) has a b_Z = 0.8 and a Z = 1%. Is there an arbitrage opportunity? If so, what will be you position on the risk-free asset? 5. The two factor model on a stock provides a risk premium for exposure to market risk of 9%, a risk premium for exposure to interest rate of (-1.3%), and a risk free rate of 3.5%. What is the expected return on the stock? 7. If enough investors decide to purchase stocks they are likely to drive up stock prices thereby causing and 6. Using the index model, the alpha of a stock is 3.0%, the beta if 1.1 and the market return is 10% What is the residual given an actual return of 15%?* 8. Security X has an expected rate of return of 16.5% and a beta of 1.15. The risk-free rate is 5% and the market expected rate of return is 15%. According to the capital asset pricing model, security X is 9. You consider buying a stock at a price of $25. The stock is expected to pay a dividend of $1.50 next year and that you can expect to sell the stoc in one year for $28. The stock's beta is 1.1, r_f is 6% and E(r_m) = 16%. What is the stock's a? * 10. Given that the o AB= O_BA, then the variance- covariance matrix for a portfolio with 50 stocks requires the calculations of variances and covariances. * 11. The beta of a security is equal to (1 Point) The covariance between the security and market returns divided by the variance of the market's returns The covariance between the security and market returns divided by the standard deviation of the market's returns The variance of the security's returns divided by the covariance between the security and market returns The variance of the security's returns divided by the variance of the market's returns 12. The standard deviation of return on investm A is . 10 while the standard deviation of return o investment B is .04. If the correlation coefficient between the returns on A and B is -.50, the covariance of returns on A and B is 17. You buy a stock for $50 per share. Over the next four months, it has monthly returns of 4%, 5%, 2%, and -3%. The value of a share at the end of the fourth month is 16. Portfolio management is primarily concerned with (1 Point) increasing return reducing risk predicting the future explaining the past 18. The variance of x is 25. What is the variance of 2x? 19. Suppose Stock A has an expected return of 15%, a standard deviation of 20%, and a Beta of 0.4 while Stock B has an expected return of 25%, a standard deviation of 30% and a beta of 1.25, and the correlation between the two stocks is 0.25. What is the standard deviation for a portfolio with 80% invested in Stock A and 20% invested in Stock B? * 20. Suppose Stock A has an expected return of 15%, a standard deviation of 20%, and a Beta of 0.4 while Stock B has an expected return of 25%, a standard deviation of 30% and a beta of 1.25, and the correlation between the two stocks is 0.25 What is the percent invested in Stock A to yield th minimum standard deviation portfolio containing Stock A and Stock B? * 27. What is the percent invested in Stock X to yield the minimum variance portfolio with Stock X and Stock Y? * 25. What is the beta for a portfolio with 60% invested in X and 40% invested in Y? * 21. Suppose Stock M has an expected return of 10%, a standard deviation of 15%, and a Beta of 0.6 while Stock N has an expected return of 20%, a standard deviation of 25% and a beta of 1.04, and the correlation between the two stocks is 0.50. What is the beta for a portfolio with 80% invested in Stock M and 20% invested in Stock N? * 23. What is the expected return for a portfolio with 60% invested in X and 40% invested in Y? * 22. The next 5 questions relate to the follov table of information: Stock X Stock Y Expected Return 14% 18% Standard Deviation 40% 54% Beta 1.20 1.50 Correlation (X,Y) = 0.25 * Option 1 Option 2