6 Root Finding 2 The spring shock system in automobiles is an example of real mechanical systems which involves the deection of nonlinear springs that would demonstrate a damping eect over time (see behavior response in Figure 4 below). The resistance force of the spring F (N), with respect to time t (s), is given by the following equation F(t) = k1(cos(t))(e t k2 ) where is a k1 and k2 are dened as spring constants (N/s). Figure 4: Damping eect with spring constants k1 = 1000 N/s and k2 = 0.6 We will use the above equation to describe the force on a cars shock system following a speed bump encountered at t = 0 seconds. We want to nd out a time instance near t = 5.5 seconds when the resistance force F is equal to zero. In order to do that, we need to nd the root values of F(t). You will nd the root values using three dierent methods. In part (6.1), you will use the Newton-Raphson method. In part (6.2), you will use the bisection method. In part (6.3), you will use the MATLAB built-in function fzero. Write a function damping with the function declaration line function S = damping(k1,k2,initialGuess) The inputs are: 7 Lab 7 Engineering 7 Fall 2018 k 1, k 2: the spring constants dened above. initialGuess: the time instance of interest, on which we want to nd a root value. The output is: S: a 1-by-1 structure array. Its eldnames and content will be described in detail in the following subproblems. In your function, represent F(t) as a function handle stored in variable F. Also, create a variable tol = 1e-6 which represents the value of the relative tolerance required for the Newton-Raphson method and the bisection method. 6.1 Newton-Raphson Within damping.m, write a subfunction myNewton with function declaration line function newton root = myNewton(f, df, x0, tol) which will iteratively calculate the root nearest to x0 given the function handle f, the function handle of the derivative of f (which you need to calculate on your own) df, the initial guess x0, and the relative tolerance tol. Store the root found using Newton-Raphson method to S in the eldname newton. 6.2 Bisection Within damping.m, write a subfunction bisection with function declaration line function bisect root = bisection(f, a, b, tol) which will iteratively calculate the root located between a and b given the function handle f, the endpoints of the range a and b, and the tolerance tol. In function damping, call subfunction bisection and use a range of initialGuess 0.5 and store the root found using bisection method to S in the eldname bisect root. MATLAB built-in function sign will be helpful here. 6.3 fzero Use fzero to determine the root of F with initialGuess as the guess location. Store the root to S in the eldname fzero root.

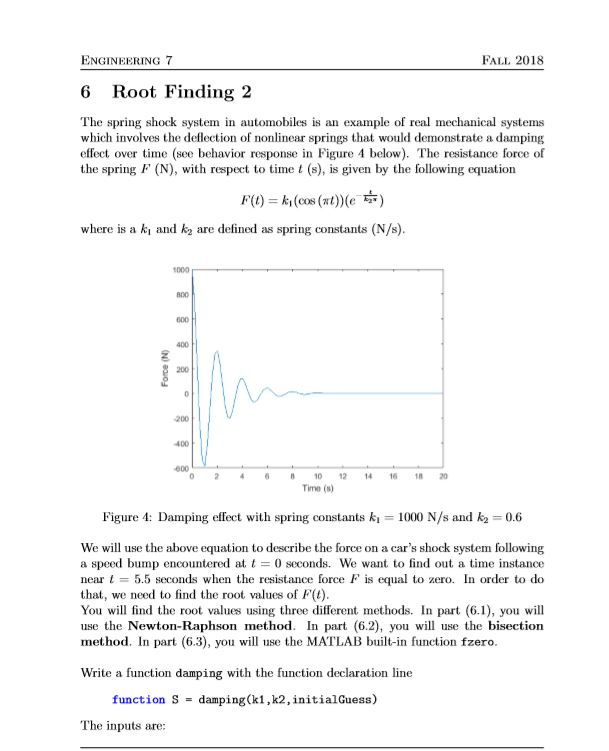
ENGINEERING 7 FALL 2018 6 Root Finding 2 The spring shock system in automobiles is an example of real mechanical systems which involves the deflection of nonlinear springs that would demonstrate a damping effect over time (see behavior response in Figure 4 below). The resistance force of the spring F (N), with respect to time t (s), is given by the following equation where is a k and k are defined as spring constants (N/s). 1000 800 400 200 00 400 600 0210 12 14 16 18 Timo () Figure : Damping effect with spring constants k 1000 N/s and k2 0.6 We will use the above equation to describe the force on a car's shock system following a speed bump encountered att 0 seconds. We want to find out a time instance near 5.5 seconds when the resistance force is equal to zero. In order to do that, we need to find the root values of F(t) You will find the root values using three different methods. In part (6), you ll use the Newton-Raphson method. In part (6.2), you wl use the bisection method. In part (6.3), you will use the MATLAB built-in function fzero. Write a function damping with the function declaration line function S damping(k1,k2, initialGuess) The inputs are: ENGINEERING 7 FALL 2018 6 Root Finding 2 The spring shock system in automobiles is an example of real mechanical systems which involves the deflection of nonlinear springs that would demonstrate a damping effect over time (see behavior response in Figure 4 below). The resistance force of the spring F (N), with respect to time t (s), is given by the following equation where is a k and k are defined as spring constants (N/s). 1000 800 400 200 00 400 600 0210 12 14 16 18 Timo () Figure : Damping effect with spring constants k 1000 N/s and k2 0.6 We will use the above equation to describe the force on a car's shock system following a speed bump encountered att 0 seconds. We want to find out a time instance near 5.5 seconds when the resistance force is equal to zero. In order to do that, we need to find the root values of F(t) You will find the root values using three different methods. In part (6), you ll use the Newton-Raphson method. In part (6.2), you wl use the bisection method. In part (6.3), you will use the MATLAB built-in function fzero. Write a function damping with the function declaration line function S damping(k1,k2, initialGuess) The inputs are