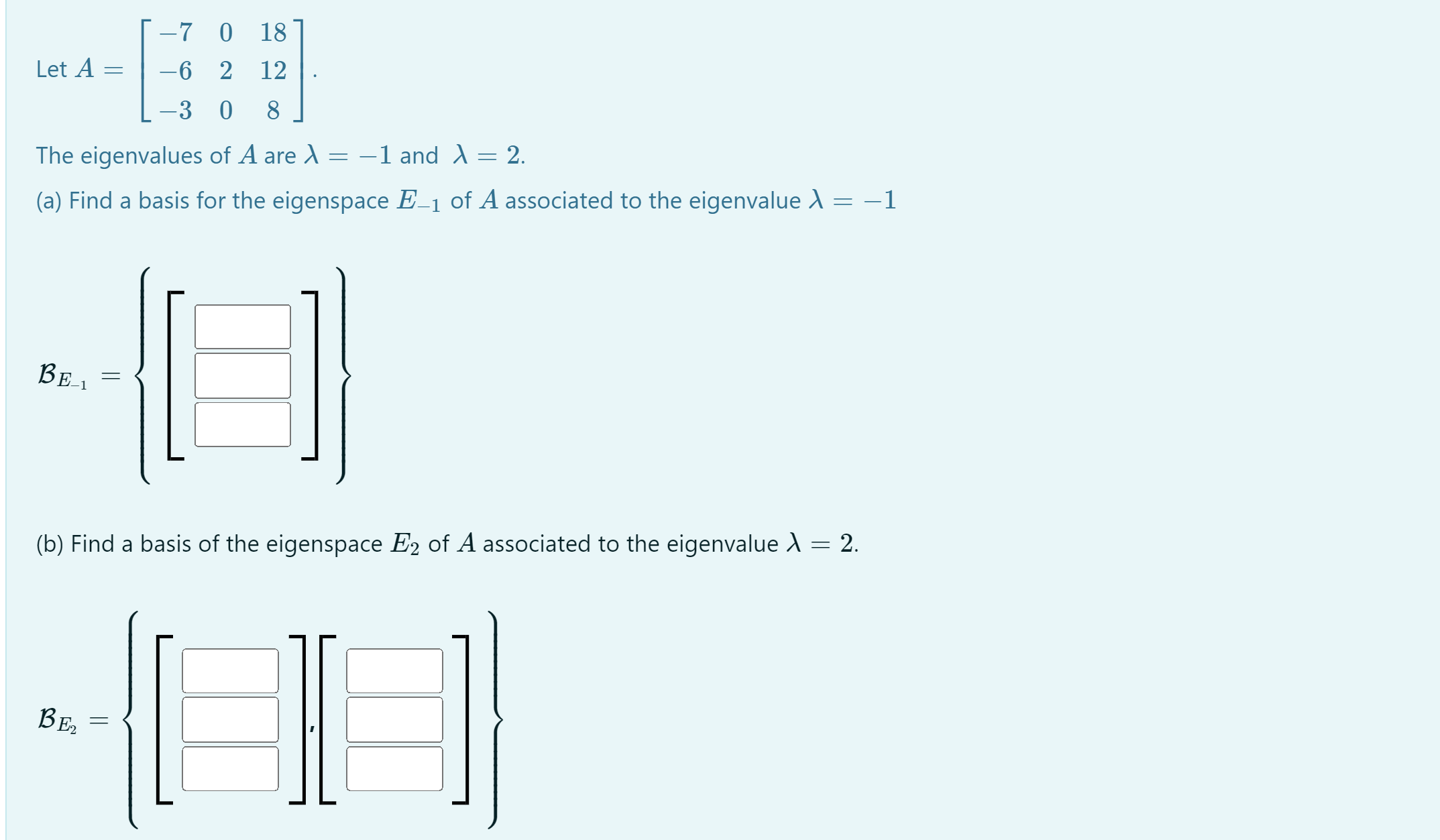
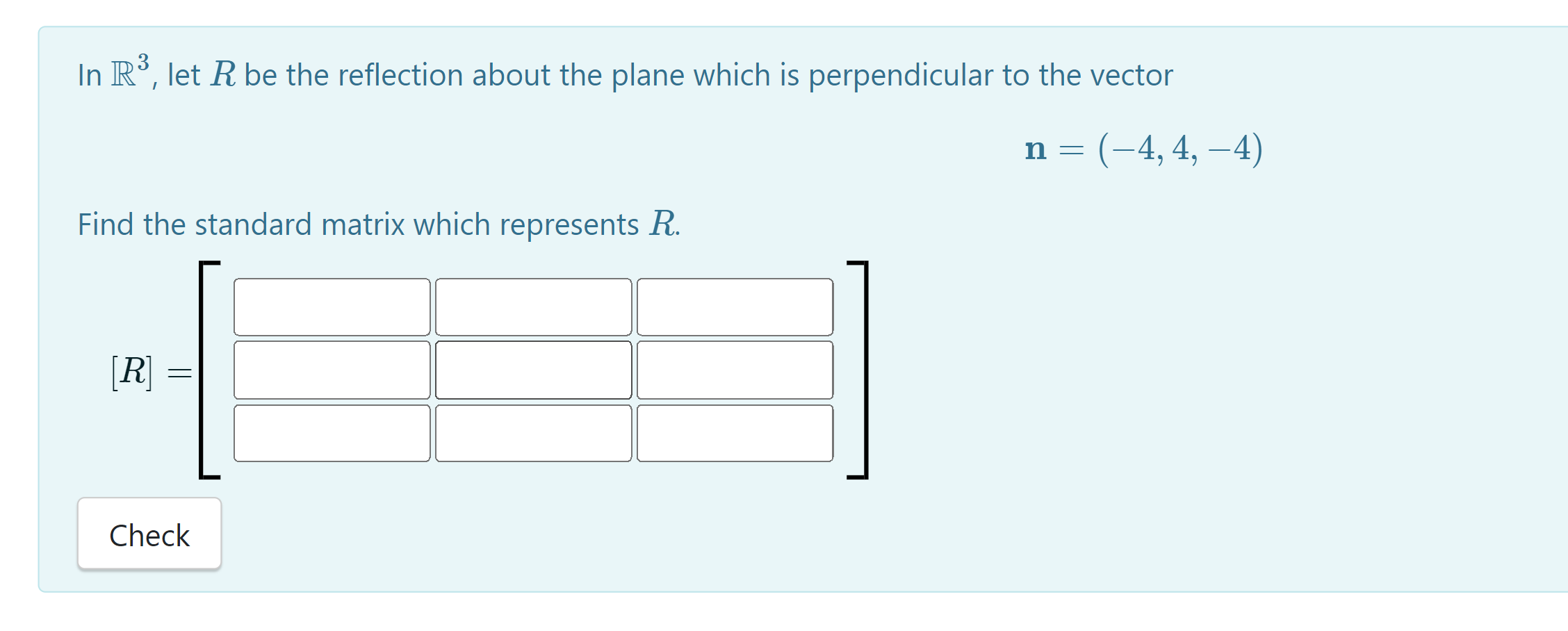
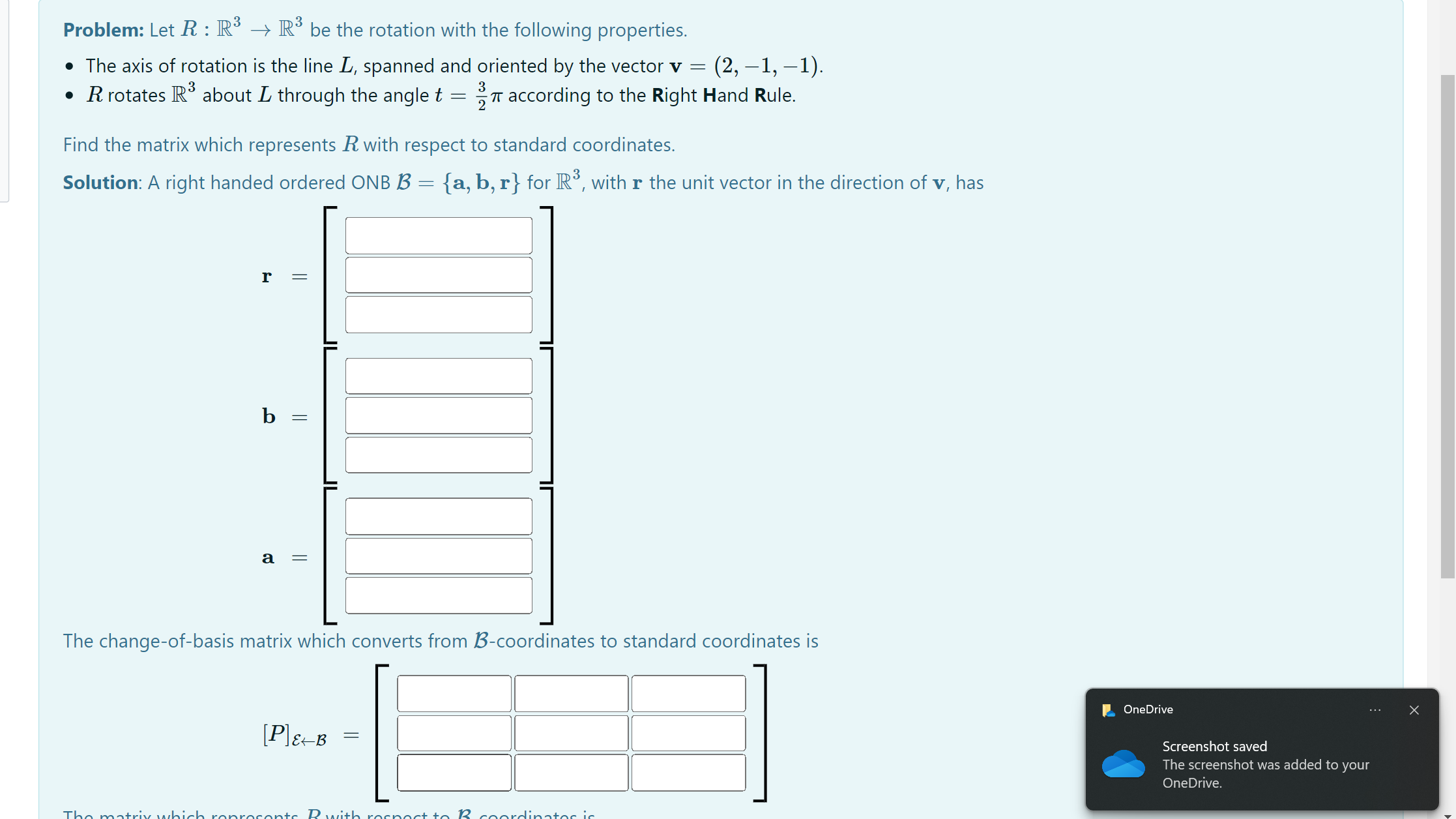
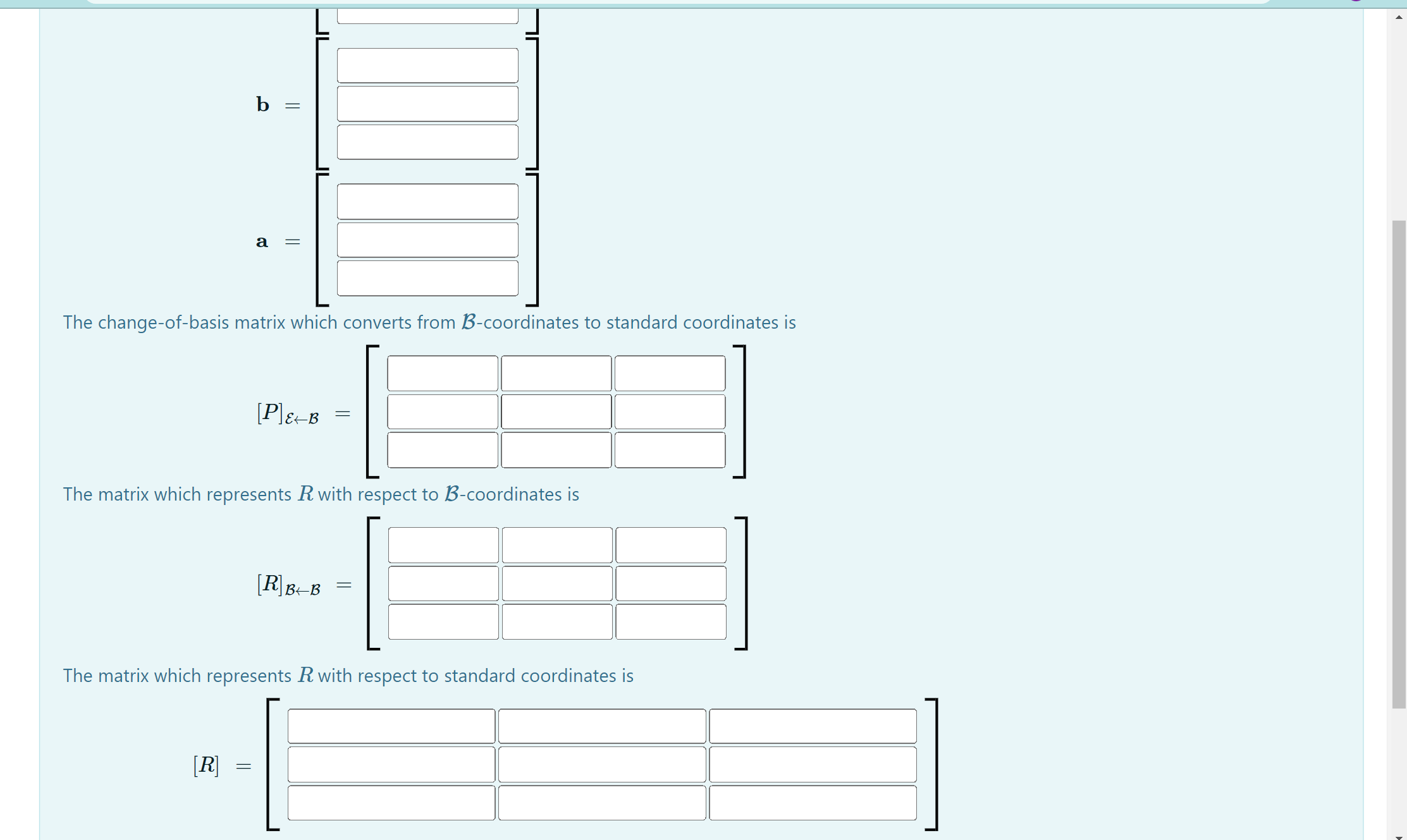
7 0 18 Let A = -6 2 12 -3 0 8 The eigenvalues of A are 1 = -1 and 1 = 2. (a) Find a basis for the eigenspace E-1 of A associated to the eigenvalue 1 = -1 BE1 = (b) Find a basis of the eigenspace E2 of A associated to the eigenvalue 1 = 2. BE2In R3, let R be the reflection about the plane which is perpendicular to the vector 11 : (4, 4, 4) Find the standard matrix which represents R. l l l l [R] = l l l l l l l J Check Problem: Let R : RS - R be the rotation with the following properties. . The axis of rotation is the line L, spanned and oriented by the vector v = (2, -1, -1). . R rotates R about L through the angle t = >7 according to the Right Hand Rule. Find the matrix which represents R with respect to standard coordinates. Solution: A right handed ordered ONB B = {a, b, r} for Ro, with r the unit vector in the direction of v, has r = b = a The change-of-basis matrix which converts from 1-coordinates to standard coordinates is OneDrive ... X [ P]&-B = Screenshot saved The screenshot was added to your OneDrive.b = a = The change-of-basis matrix which converts from 1-coordinates to standard coordinates is [Ple B = The matrix which represents R with respect to B-coordinates is [ R] B -B The matrix which represents R with respect to standard coordinates is [R] =