7

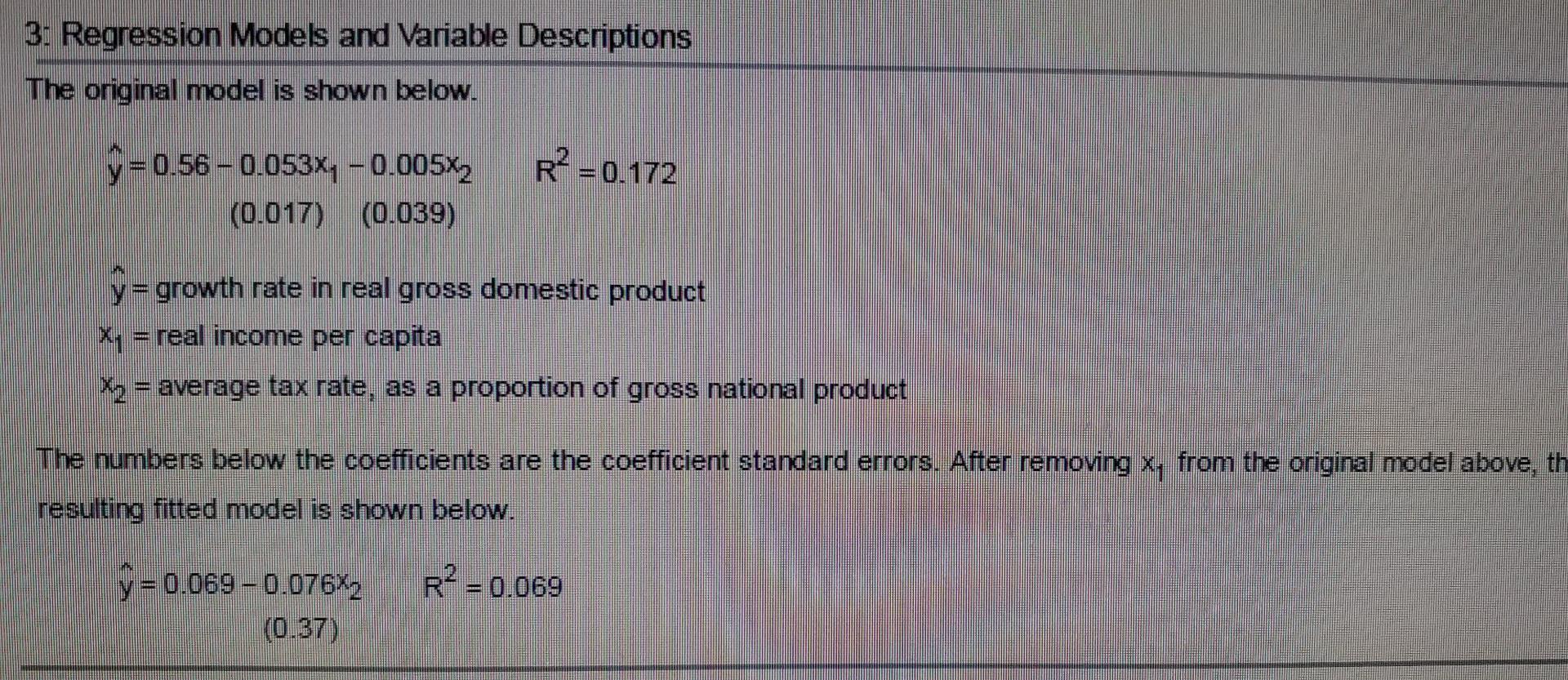
7. Based on the data from 63 countries, a model was estimated by least squares. After the independent variable x was dropped from the model, the regression of growth rate in real gross domestic product on x2 was estimated and the new fitted model was found. * Click the icon to see the regression models and varieble descriptions. Comment on the change in the coefficient of x2 as x; is removed from the model. Choose the correct answer below. O A. The large change in the coefficient of X, as X, is removed from the model is an indicator of the likely presence of multicolnearity in the original model. When there is multicollinearity in a model, the coefficients of the collinear variables often change drastically from their true values and can even change signs. O B. The large change in the coefficient of x2 as x, is removed from the model is an indicator that there is no multicollinearity in the original model. Whenever an independent variable is Oc. The change in the coefficient of X2 indicates neither a presence nor a lack of multicollinearity in the original model. Changes in the estimates of the coefficients could be the result of many factors and there is not enough information given to say that this change resulted from multicollinearity. Comment on the change in the standard error of the coefficient of x2 as x, is removed from the model. Choose the correct answer below. O A. The increase in the x, coefficient standard error as x, is removed seems to indicate the presence of multicolinearity in the model. A model with collinear independent variables often has small coefficient standard errors and removing a collinear vanable should increase the standard errors of the coefficients of the remaining collinear variables. O B. The increase in the xz coefficient standard error as x, is removed seems to indicate a lack of multicollinearity in the model. A model with collinear independent variables often has large coefficient standard errors and removing a collinear variable should reduce the standard errors of the coefficients of the remaining collinear variables C. The increase in the x2 coefficient standard error as Xi is removed indicates neither a presence nor a lack of multicollinearity in the original model. Whenever an independent variable is removed from a regression equation, the remaining coefficient standard errors will always increase Comment on the change in RP as x, is removed from the model. Choose the correct answer below. O A. The change in R is an indicator of the lack of multicollinearity. Whenever an independent variable is removed from a model, the value of R2 will only increase if the original model contained collinear variables. OB. The change in R is expected. Whenever an independent variable is removed from a model, the value of R2 will always decrease unless the coefficient was exactly zero. Oc. The change in R2 is an indicator of the presence of multicollinearity. Whenever an independent variable is removed from a model the value of R will only decrease if the original model contained collinear variables Summarize your comments on the presence of multicollinearity in the regression model. Choose the correct answer below. A. The results indicate a likely presence of multicollinearity in the onginal model. The changes in Rthe magnitude of the coefficient of xy, and the coefficient standard error all indicate that there is multicollinearity in the model. OB. The results are inconclusive. There may or may not be multicollinearity in the original model. 3: Regression Models and Variable Descriptions The original model is shown below. R? -0.172 =0.56 -0.053x, -0.005x2 (0.017) (0.039) y=growth rate in real gross domestic product Xy = real income per capita X2 = average tax rate, as a proportion of gross national product The numbers below the coefficients are the coefficient standard errors. After removing x, from the original model above, th resulting fitted model is shown below. R = 0.069 y=0.069 -0.076X2 (0.37)