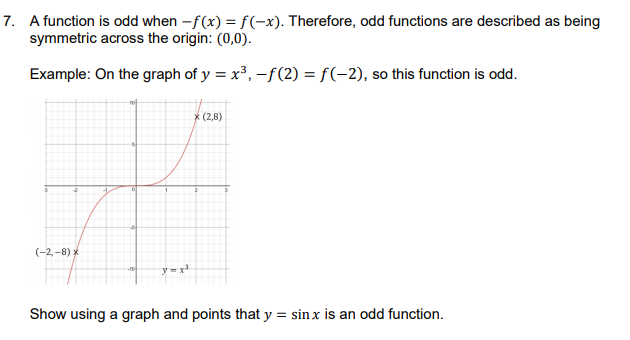
7. A function is odd when -f(x) = f(-x). Therefore, odd functions are described as being symmetric across the origin: (0,0). Example: On the graph of y = x3, -f(2) = f(-2), so this function is odd. * (2,B) (-2,-8) * Show using a graph and points that y = sin x is an odd function.6. A function is even when f(x) = f(-x). Therefore, even functions are symmetric across the y-axis or can be said to reflect across the y-axis. Example: On the graph of y = x2, f(2) = f(-2), so this function is even. (-2,4) * * (2.4) 2 Show using a graph and points that y = cos x is an even function