np.array: computes matrix-vector multiplication via the width=1149 height=398> 7 Defining Matrix-Vector Multiplication Your- self (Programming) (15 points) This week you will be writing your

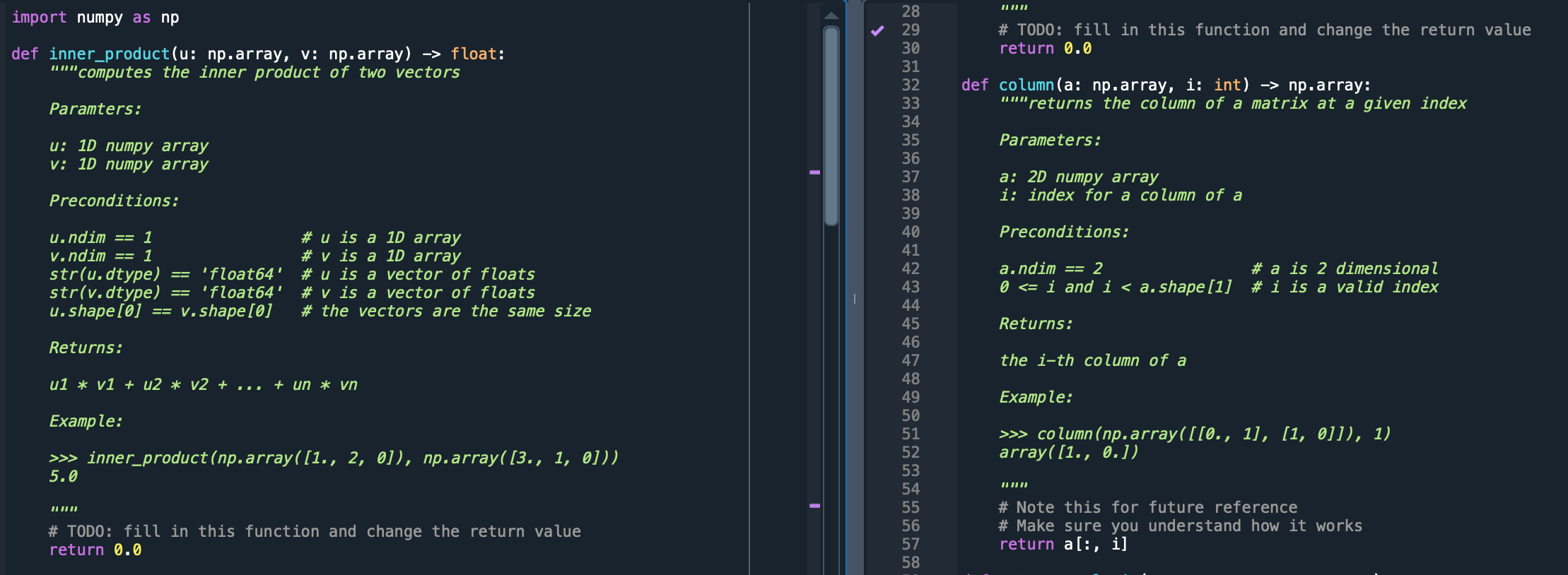
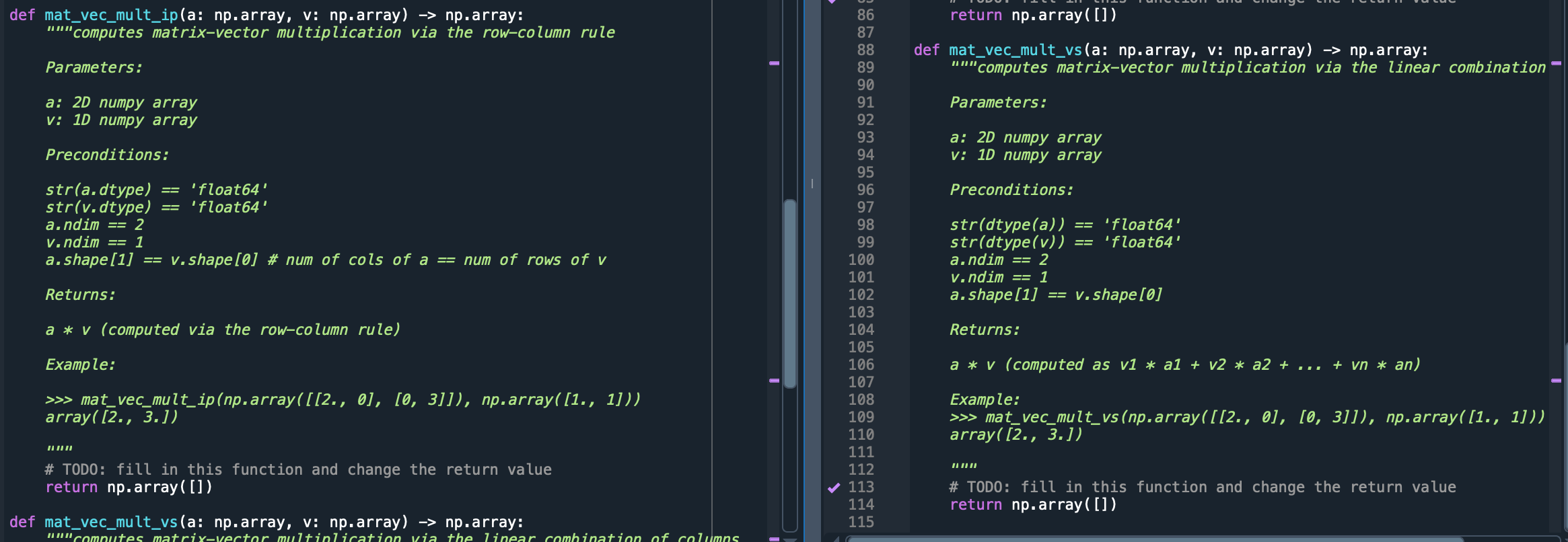
7 Defining Matrix-Vector Multiplication Your- self (Programming) (15 points) This week you will be writing your own definition of matrix-vector multiplication in Python. This will give you the opportunity to work with numpy arrays directly if you haven't already (all your previous assignments have only required indirect use of numpy arrays). Read through the docstring of each function carefully. You are given starter code in the file hw04prog.py. Don't change the name of this file when you submit. Also don't change the names of the functions included in the starter code. The only changes you should make are to fill in the TODO items in the starter code. There are three functions you need to fill in. inner_product, which computes the inner product of two vectors. Recall that the inner product, also called the dot product, is defined as 212 0.0 Un = U1V + U2V + + Un n = UV Vn i=1 mat_vec_mult_ip, which computes matrix-vector multiplication using the row-column rule and inner products: a11 a12 021 022 : aml am2 [a 82 ain a2n an amn V V1 V2 Zi=1 amivi] Recall that the rows of a numpy array are themselves numpy arrays, so you should be able to use your inner product function directly here. mat-vec-mult_vs, which computes matrix-vector multiplication, but using the definition we gave in class: V1 U2 = Un " =1 alivi Zi=192ivi : = V + V2 + + Vnn Of course, the last two functions will compute the same vector, but they will do so in different ways. The first should compute each entry of the output vector individually, whereas the second should compute a linear combination of the columns of the given matrix using addition and scaling of numpy arrays. For this assignment you are not allowed use built in numpy functions for inner products or matrix-vector multiplication, like np.inner or np. dot or . The point is for you to implement your own. You will upload the single python file hw04prog.py to Gradescope with your implementations of the required functions. We will be running autograder tests on your submission to determine its correctness. You will not have access to the autograder tests. 7 Defining Matrix-Vector Multiplication Your- self (Programming) (15 points) This week you will be writing your own definition of matrix-vector multiplication in Python. This will give you the opportunity to work with numpy arrays directly if you haven't already (all your previous assignments have only required indirect use of numpy arrays). Read through the docstring of each function carefully. You are given starter code in the file hw04prog.py. Don't change the name of this file when you submit. Also don't change the names of the functions included in the starter code. The only changes you should make are to fill in the TODO items in the starter code. There are three functions you need to fill in. inner_product, which computes the inner product of two vectors. Recall that the inner product, also called the dot product, is defined as 212 0.0 Un = U1V + U2V + + Un n = UV Vn i=1 mat_vec_mult_ip, which computes matrix-vector multiplication using the row-column rule and inner products: a11 a12 021 022 : aml am2 [a 82 ain a2n an amn V V1 V2 Recall that the rows of a numpy array are themselves numpy arrays, so you should be able to use your inner-product function directly here. mat-vec-mult_vs, which computes matrix-vector multiplication, but using the definition we gave in class: V1 U2 = Un " =1 alivi Zi=192ivi : Zi=1 ami vi] = V + V2 + + Vnn Of course, the last two functions will compute the same vector, but they will do so in different ways. The first should compute each entry of the output vector individually, whereas the second should compute a linear combination of the columns of the given matrix using addition and scaling of numpy arrays. For this assignment you are not allowed use built in numpy functions for inner products or matrix-vector multiplication, like np.inner or np. dot or . The point is for you to implement your own. You will upload the single python file hw04prog.py to Gradescope with your implementations of the required functions. We will be running autograder tests on your submission to determine its correctness. You will not have access to the autograder tests.