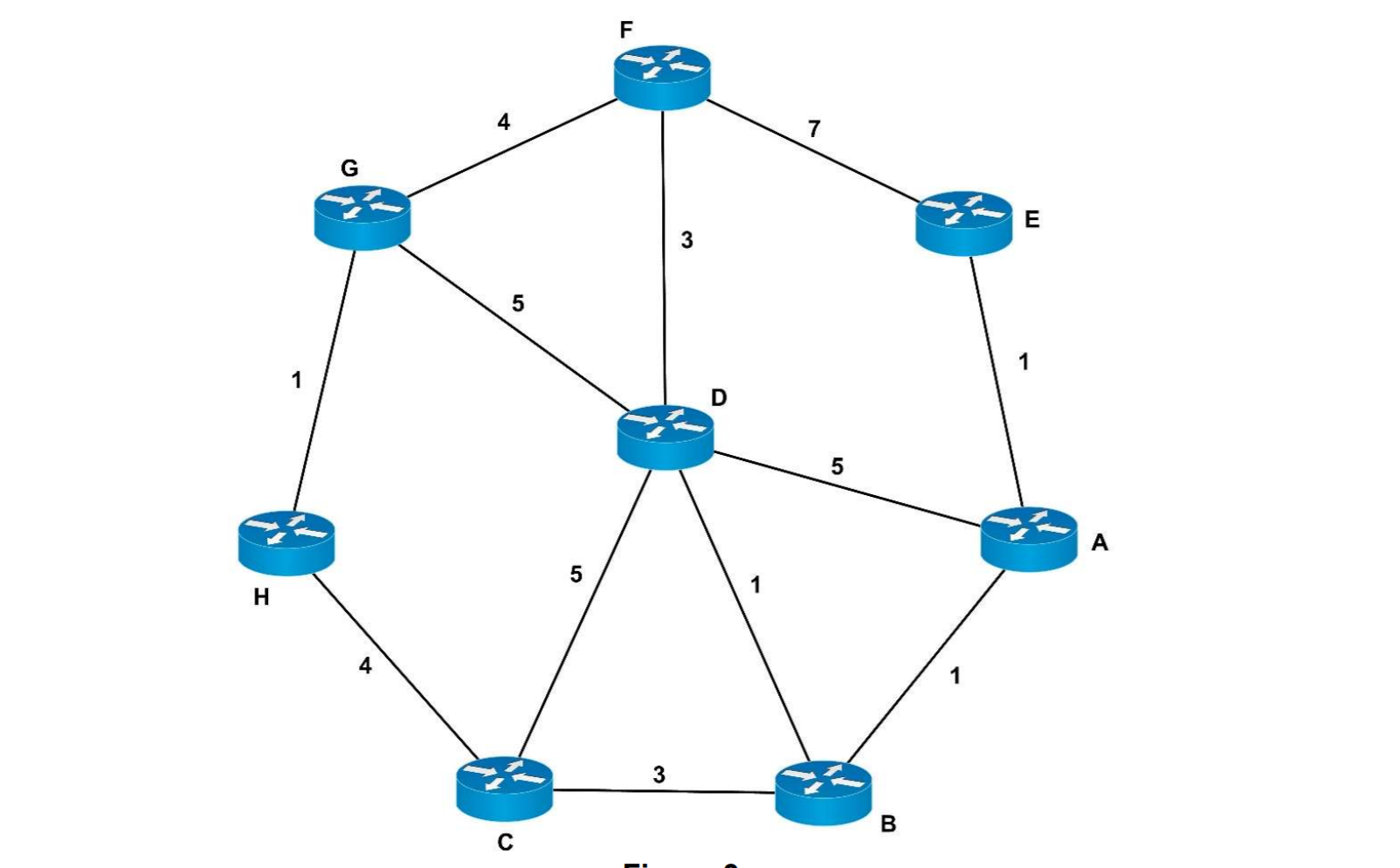
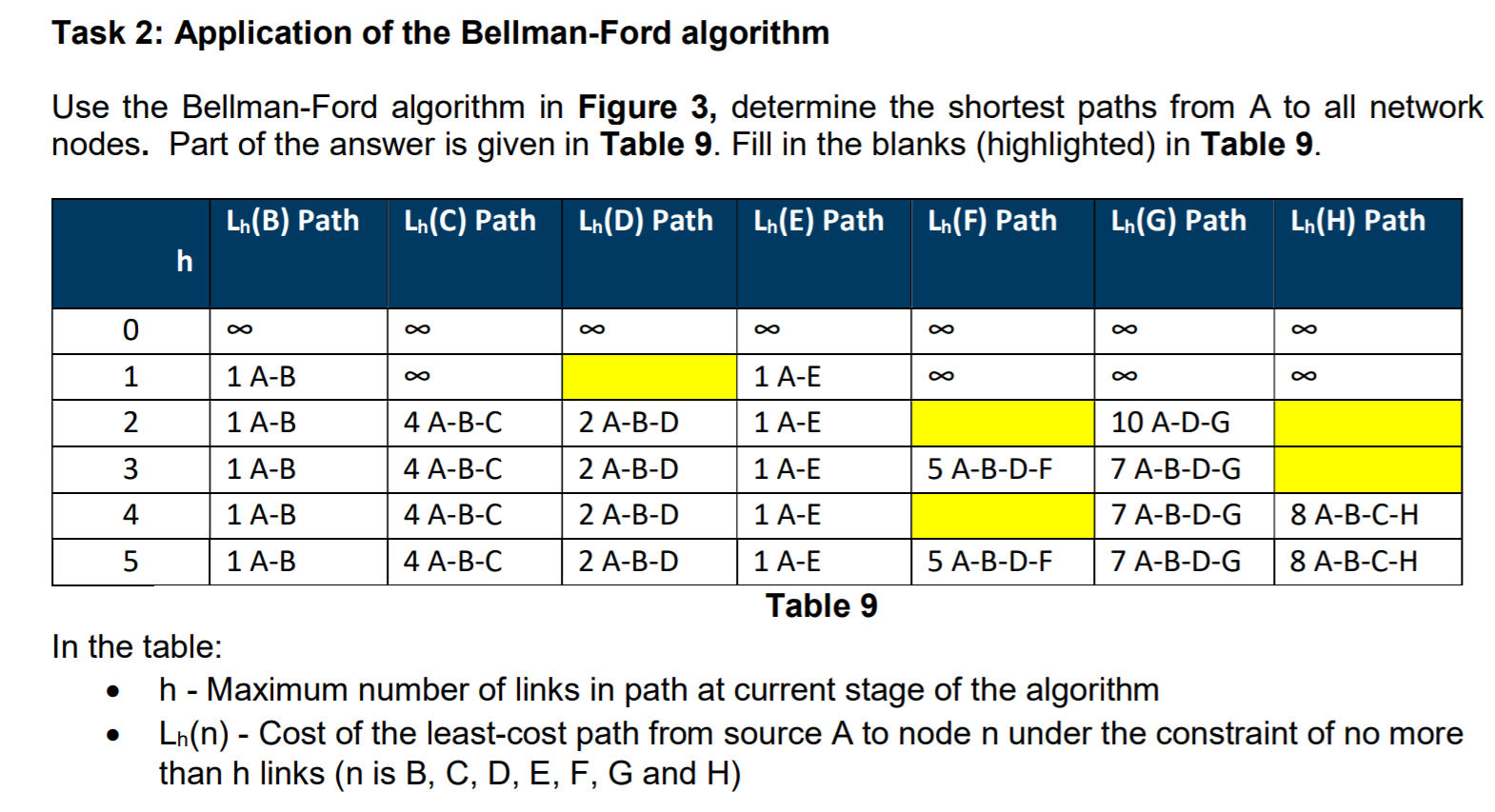
7 G E 3 5 1 1 D 5 5 H 3 B Task 2: Application of the Bellman-Ford algorithm Use the Bellman-Ford algorithm in Figure 3, determine the shortest paths from A to all network nodes. Part of the answer is given in Table 9. Fill in the blanks (highlighted) in Table 9. Lh(B) Path Lh(C) Path Lh(D) Path Lh(E) Path Lh(F) Path Lh(G) Path Lh(H) Path h O ~ ~ ~ ~ 1 1 A-B 1 A-E 2 1 A-B 4 A-B-C 2 A-B-D 1 A-E 10 A-D-G 3 1 A-B 4 A-B-C 2 A-B-D 1 A-E 5 A-B-D-F 7 A-B-D-G 4 1 A-B 4 A-B-C 2 A-B-D 1 A-E 7 A-B-D-G 8 A-B-C-H 5 1 A-B 4 A-B-C 2 A-B-D 1 A-E 5 A-B-D-F 7 A-B-D-G 8 A-B-C-H Table 9 In the table: h - Maximum number of links in path at current stage of the algorithm Ln(n) - Cost of the least-cost path from source A to node n under the constraint of no more than h links (n is B, C, D, E, F, G and H)