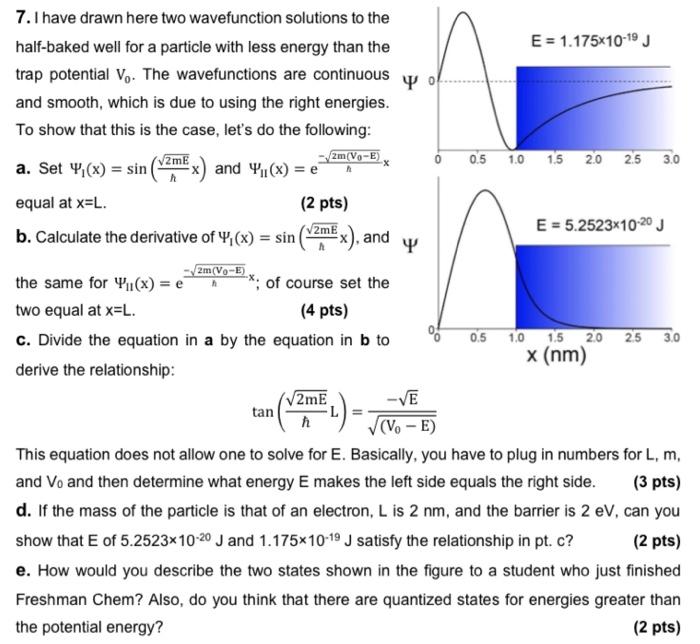
7. I have drawn here two wavefunction solutions to the half-baked well for a particle with less energy than the trap potential V0. The wavefunctions are continuous and smooth, which is due to using the right energies. To show that this is the case, let's do the following: a. Set 1(x)=sin(h2mEx) and 1I(x)=eh2m(V0E)x equal at x=L. (2 pts) b. Calculate the derivative of 1(x)=sin(h2mEx), and the same for 11(x)=eh2m(V0E)x; of course set the two equal at x=L. (4 pts) c. Divide the equation in a by the equation in b to derive the relationship: tan(2mEL)=(V0E)E This equation does not allow one to solve for E. Basically, you have to plug in numbers for L,m, and V0 and then determine what energy E makes the left side equals the right side. (3 pts) d. If the mass of the particle is that of an electron, L is 2nm, and the barrier is 2eV, can you show that E of 5.25231020J and 1.1751019J satisfy the relationship in pt. c? (2 pts) e. How would you describe the two states shown in the figure to a student who just finished Freshman Chem? Also, do you think that there are quantized states for energies greater than the potential energy? (2 pts)