Question: 7. Let A = 2, B = 5, C = 1 and A' = 3, B' = -1, C' = 2 be two groups of

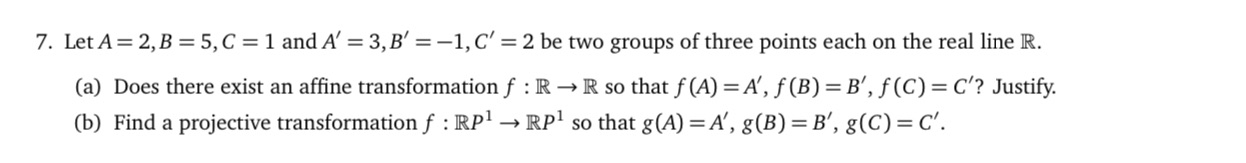
7. Let A = 2, B = 5, C = 1 and A' = 3, B' = -1, C' = 2 be two groups of three points each on the real line R. (a) Does there exist an affine transformation f : R - R so that f (A) = A', f (B) = B', f(C) = C'? Justify. (b) Find a projective transformation f : RP] - RP so that g (A) = A', g(B) = B', g(C) = C'

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

2/12/2017 Unit 1 Homework Assignment (2.1, 2.2, 2.3, 2.4) WebAssign Unit 1 Homework Assignment (2.1, 2.2, 2.3, 2.4) (Homework) Current Score : 2 / 40 Shadi Hanna MAT230, section MAT230.30 MOD3 2017,...

1. Choose correct answer. 1. The following are notations for composite functions EXCEPT, a. h(p(x)) b. f(x)g(x) C. (s o t) (x) d. f(g(x)) 2. Find h(3) + d(2) if h(x) = x -1 and d(x) = 7x +3 b. 2 b. 5...

University of Illinois Chicago Department of Economics B ECON120: Principles of Microeconomics BC Spring, 2023 Midterm 2 (Form 1) BC First Name: Last Name: UIN: B 1 2 There are two parts in this...

Module 1 Direction. Write the letter of the correct answer on a separate answer sheet. 1. The following are notations for composite functions EXCEPT, a. h(p(x)) b. f(x)g(x) C. (5 . t ) (x) d. f(g(x)...

When you undertake large, complicated projects like building a house, developing a new product, or getting your children ready for school, it can be helpful to understand network management. Chapter...

Please answer the 9 questions, and for any formulas, PLEASE only use the formula sheet provided. Mathematics 30-1 Formula Sheet For ax' + bx + c = 0, Trigonometry x = =bzyb - 4ac 2a 0 = a Relations...

There are two assignments (below). Your assignment is to do the following problems at the end of chapter 11. You will have to either draw a picture in Word or take a picture and attach it so I can...

You must show your work on your submission in order to receive credit! #3.6 Given the activities whose sequence is described by the following table, draw the appropriate activity- on-arrow (AOA)...

There is no need to give an explanation, please only give correct answers. Also, please answer all questions as this is very important. 1. After passing through a 24-V battery, a charge of 5C gains...

Question 4 There are 28 students in Mr. Connelly's Grade 12 mathematics class. Not yet The number of students in the yearbook club and the number of students on student council are answered shown in...

If one of the subjects is randomly selected, find the probability of selecting someone who did not wear a helmet or was not injured. Head injured Head not injured Wore helmet No helmet 656 2330

Assess Corbin Churchs plan for selling Miche bags. How was changing his approach from franchising to a direct sales home party approach a more effective strategic plan?

3 0 . The generation - skipping transfer tax applies to all of the following types of transfers except: Group of answer choices Direct skips. Transfers to grandchildren whose parents are deceased....

On 1 March 2007 DB Limited issued R560 000 15% debentures at R98. The debentures were to be redeemed at par in four equal annual payments starting 28 February 2010. Required: Journalise the above...