7. This exercise was also contributed by Dr. Rick Wilson of Oklahoma State University.

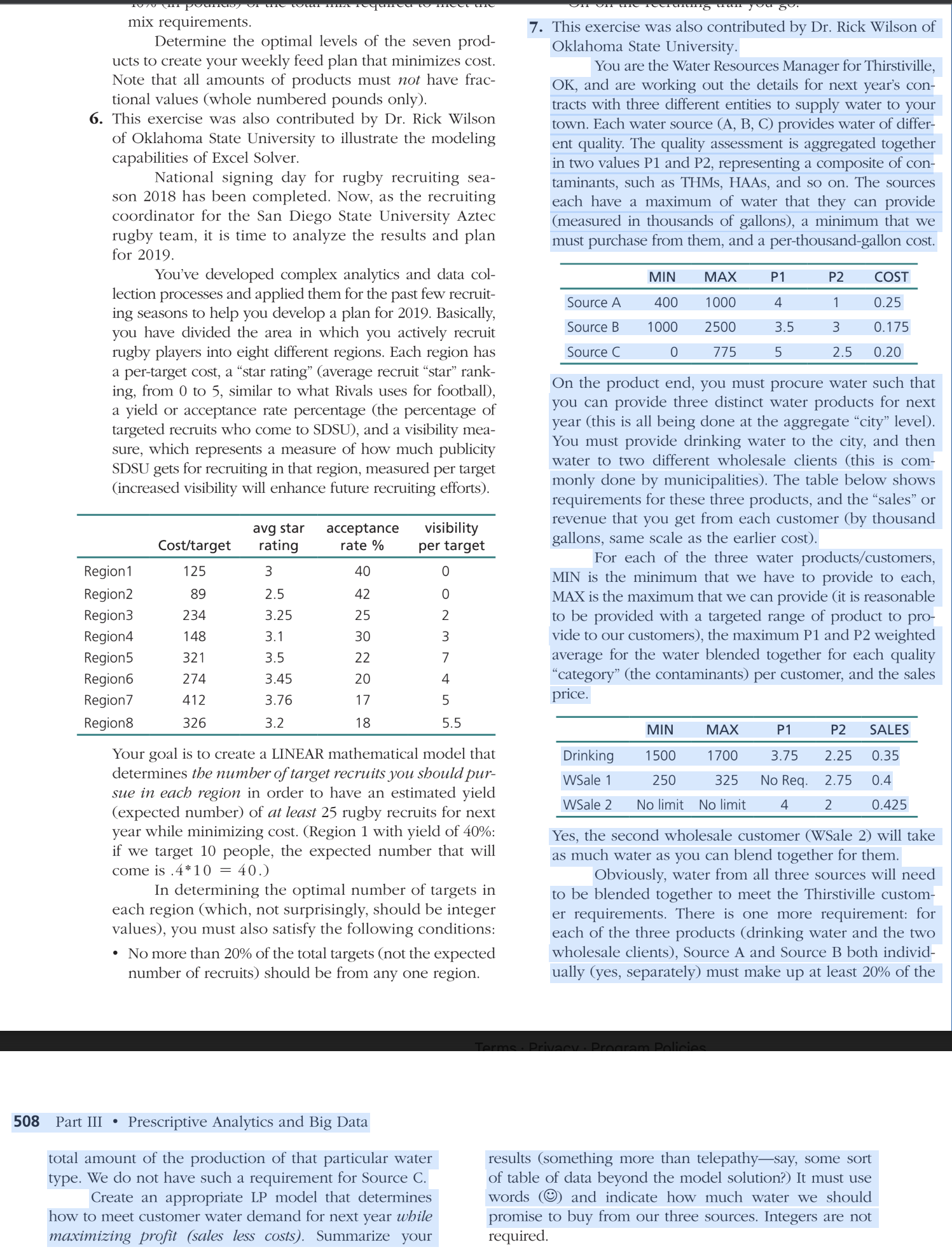
You are the Water Resources Manager for Thirstiville, OK, and are working out the details for next years con- tracts with three different entities to supply water to your town. Each water source (A, B, C) provides water of differ- ent quality. The quality assessment is aggregated together in two values P1 and P2, representing a composite of con- taminants, such as THMs, HAAs, and so on. The sources each have a maximum of water that they can provide (measured in thousands of gallons), a minimum that we must purchase from them, and a per-thousand-gallon cost.

MIN MAX P1 P2 COST Source A 400 1000 4 1 0.25 Source B 1000 2500 3.5 3 0.175 Source C 0 775 5 2.5 0.20

On the product end, you must procure water such that you can provide three distinct water products for next year (this is all being done at the aggregate city level). You must provide drinking water to the city, and then water to two different wholesale clients (this is commonly done by municipalities). The table below shows requirements for these three products, and the sales or revenue that you get from each customer (by thousand gallons, same scale as the earlier cost).

For each of the three water products/customers, MIN is the minimum that we have to provide to each, MAX is the maximum that we can provide (it is reasonable to be provided with a targeted range of product to pro- vide to our customers), the maximum P1 and P2 weighted average for the water blended together for each quality category (the contaminants) per customer, and the sales price.

MIN MAX P1 P2 SALES Drinking 1500 1700 3.75 2.25 0.35 WSale 1 250 325 No Req. 2.75 0.4 WSale 2 No limit No limit 4 2 0.425

Yes, the second wholesale customer (WSale 2) will take as much water as you can blend together for them.

Obviously, water from all three sources will need to be blended together to meet the Thirstiville custom- er requirements. There is one more requirement: for each of the three products (drinking water and the two wholesale clients), Source A and Source B both individually (yes, separately) must make up at least 20% of the 508 Part III Prescriptive Analytics and Big Data total amount of the production of that particular water type. We do not have such a requirement for Source C.

Create an appropriate LP model that determines how to meet customer water demand for next year while maximizing profit (sales less costs). Summarize your results (something more than telepathysay, some sort of table of data beyond the model solution?) It must use words ( ) and indicate how much water we should promise to buy from our three sources. Integers are not required.

Need help with using Solver in Excel

mix requirements. Determine the optimal levels of the seven products to create your weekly feed plan that minimizes cost. Note that all amounts of products must not have fractional values (whole numbered pounds only). 6. This exercise was also contributed by Dr. Rick Wilson of Oklahoma State University to illustrate the modeling capabilities of Excel Solver. National signing day for rugby recruiting season 2018 has been completed. Now, as the recruiting coordinator for the San Diego State University Aztec rugby team, it is time to analyze the results and plan for 2019. You've developed complex analytics and data collection processes and applied them for the past few recruiting seasons to help you develop a plan for 2019. Basically, you have divided the area in which you actively recruit rugby players into eight different regions. Each region has a per-target cost, a "star rating" (average recruit "star" ranking, from 0 to 5 , similar to what Rivals uses for football), a yield or acceptance rate percentage (the percentage of targeted recruits who come to SDSU), and a visibility measure, which represents a measure of how much publicity SDSU gets for recruiting in that region, measured per target (increased visibility will enhance future recruiting efforts). Your goal is to create a LINEAR mathematical model that determines the number of target recruits you should pursue in each region in order to have an estimated yield (expected number) of at least 25 rugby recruits for next year while minimizing cost. (Region 1 with yield of 40% : if we target 10 people, the expected number that will come is .410=40.) In determining the optimal number of targets in each region (which, not surprisingly, should be integer values), you must also satisfy the following conditions: - No more than 20% of the total targets (not the expected number of recruits) should be from any one region. 7. This exercise was also contributed by Dr. Rick Wilson of Oklahoma State University. You are the Water Resources Manager for Thirstiville, OK, and are working out the details for next year's contracts with three different entities to supply water to your town. Each water source (A, B, C) provides water of different quality. The quality assessment is aggregated together in two values P1 and P2, representing a composite of contaminants, such as THMs, HAAs, and so on. The sources each have a maximum of water that they can provide (measured in thousands of gallons), a minimum that we must purchase from them, and a per-thousand-gallon cost. On the product end, you must procure water such that you can provide three distinct water products for next year (this is all being done at the aggregate "city" level). You must provide drinking water to the city, and then water to two different wholesale clients (this is commonly done by municipalities). The table below shows requirements for these three products, and the "sales" or revenue that you get from each customer (by thousand gallons, same scale as the earlier cost). For each of the three water products/customers, MIN is the minimum that we have to provide to each, MAX is the maximum that we can provide (it is reasonable to be provided with a targeted range of product to provide to our customers), the maximum P1 and P2 weighted average for the water blended together for each quality "category" (the contaminants) per customer, and the sales price. Yes, the second wholesale customer (WSale 2) will take as much water as you can blend together for them. Obviously, water from all three sources will need to be blended together to meet the Thirstiville customer requirements. There is one more requirement: for each of the three products (drinking water and the two wholesale clients), Source A and Source B both individually (yes, separately) must make up at least 20% of the 8 Part III Prescriptive Analytics and Big Data total amount of the production of that particular water type. We do not have such a requirement for Source C. Create an appropriate LP model that determines how to meet customer water demand for next year while maximizing profit (sales less costs). Summarize your results (something more than telepathy-say, some sort of table of data beyond the model solution?) It must use words (-)) and indicate how much water we should promise to buy from our three sources. Integers are not required