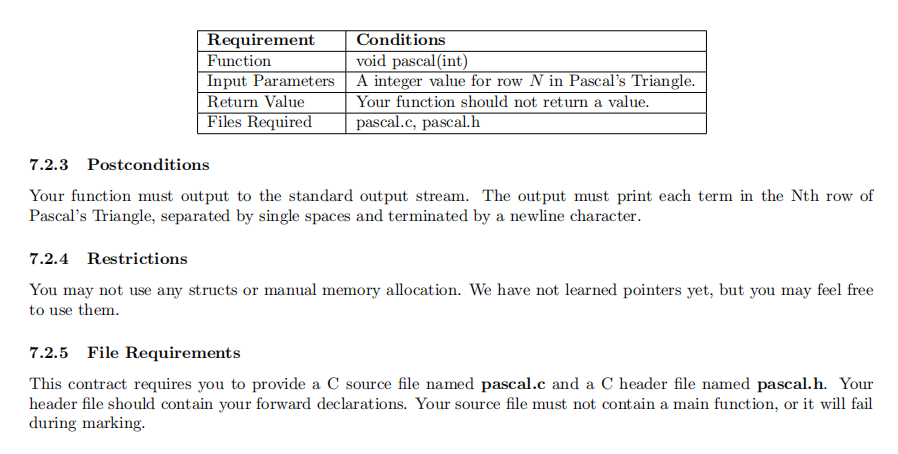
7.2 Pascal 7.2.1 Problem Given a integer, print that row of Pascal's Triangle. 7. 2. 2 Preconditions You must provide a single function which meets the require- ments in the table below. You you may include other func tions as long as the requested function executes correctly. Do not include a main function in your source or header les. Pascal's Triangle is an array of numbers which are structured as a downwardgrowing triangle which is often used to show a recurrence relation between a number of choices and how many ways we can se- lect subsets of those choices, typically referred to as combinations, which are a focus of the eld of combinatorics. The triangle has many interesting properties, such as each row summing to a power of 2, justied diagonals of the triangle summing to the Fibonacci sequence, and each row's digits concatenating to powers of 11. The feature of the triangle we will focus on here is the triangles ability to tell us how many different ways we can select K items from a pool of N items. We usually write this question in the form of N choose K, which is written as {g} in mathematics. A single row N in Pascal's Triangle contains N + 1 terms, where each term is counted using K from left to right. K, therefore, has a range of [0, N]. By moving along a row with Pascal's Triangle, each term tells us how many items we can choose from a pool with increasing numbers of selections. For example, the fourth row (starting from row 0) of Pascal's Triangle contains the terms 1,4,,4, 1. This means that if we have 4 items to choose from, but we can only choose 3 (which is (:1), we can look at the 4th term in the list and see that there are 4 ways to select from those items, amuming we don't care what order they're chosen in. It's also worth noting that the rst K term is O, and there's only one way to choose no items from the pool. 0n the other hand, the last K term is N, and there's only one way to choose all of the items from any item pool. It turns out that the equation for determining a Ki}: term in an Nth row is recurrent, which means it looks at a previous row to determine its Value. Any value in the triangle is the sum of the two 1aalues directly above it to the left and right. This is usually written as: ()=(Zi)+(r1)=$ ( ) Requirement Conditions Function void pascal (int) Input Parameters A integer value for row N in Pascal's Triangle. Return Value Your function should not return a value. Files Required pascal.c, pascal.h 7.2.3 Postconditions Your function must output to the standard output stream. The output must print each term in the Nth row of Pascal's Triangle, separated by single spaces and terminated by a newline character. 7.2.4 Restrictions You may not use any structs or manual memory allocation. We have not learned pointers yet, but you may feel free to use them. 7.2.5 File Requirements This contract requires you to provide a C source file named pascal.c and a C header file named pascal.h. Your header file should contain your forward declarations. Your source file must not contain a main function, or it will fail during marking