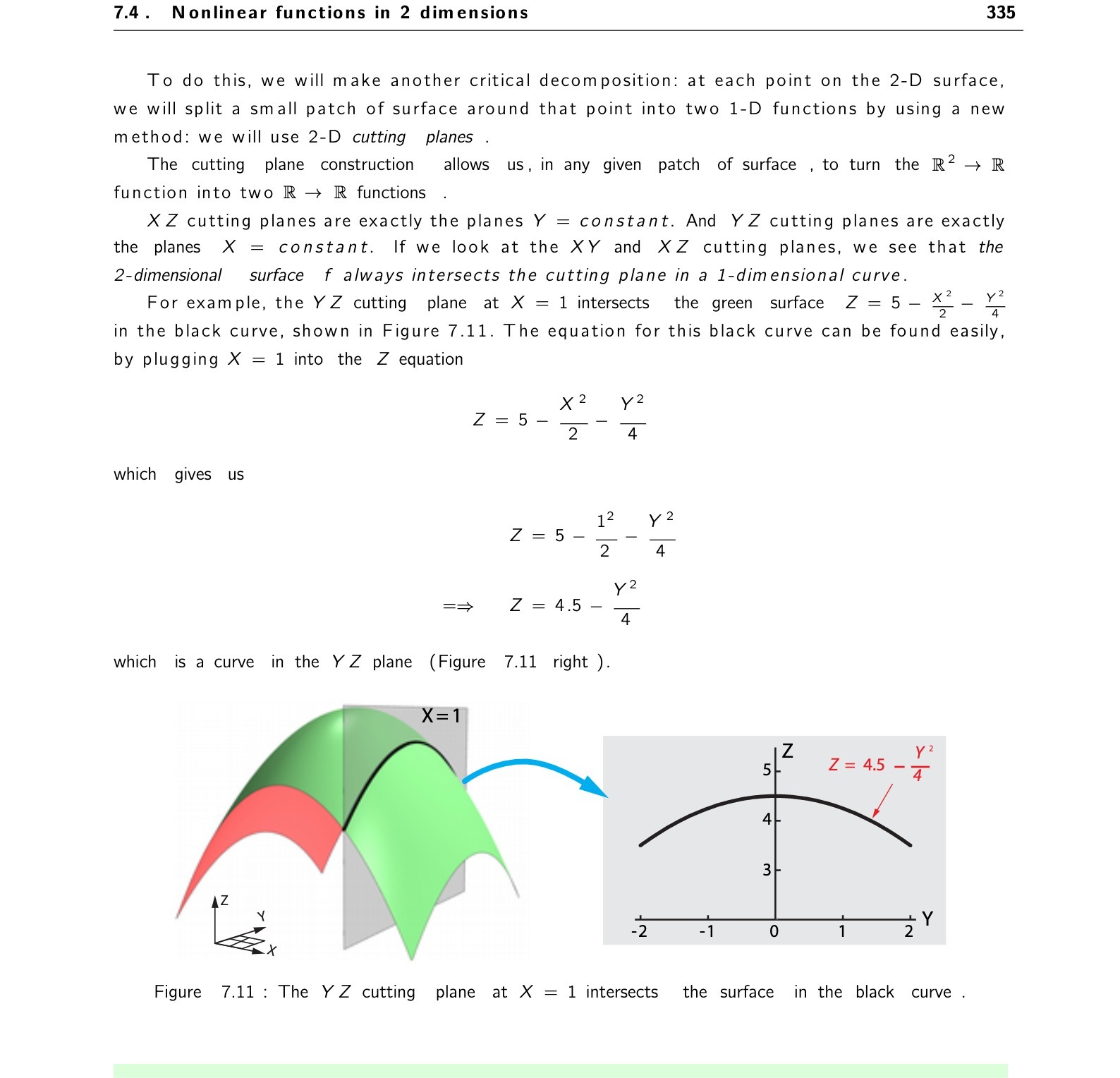
Question: 7.4. Nonlinear functions in 2 dimensions 335 To do this, we will make another critical decomposition: at each point on the 2D surface, we will
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


