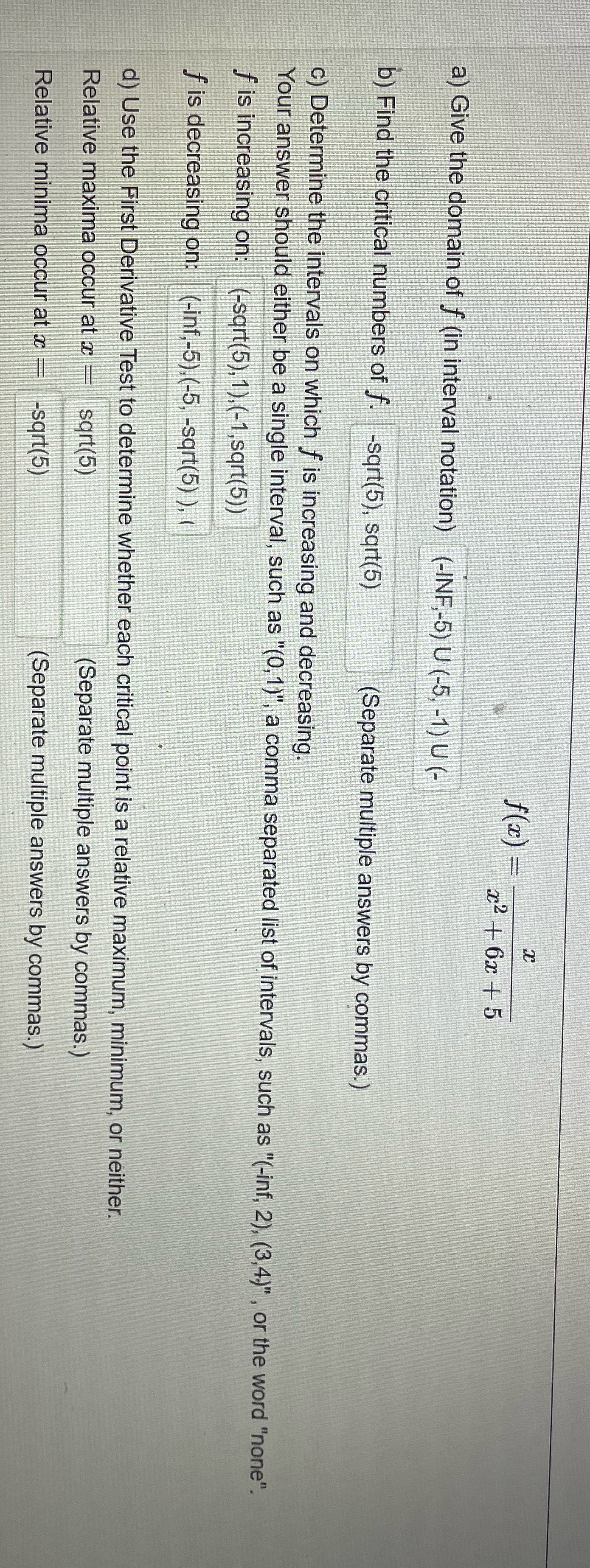
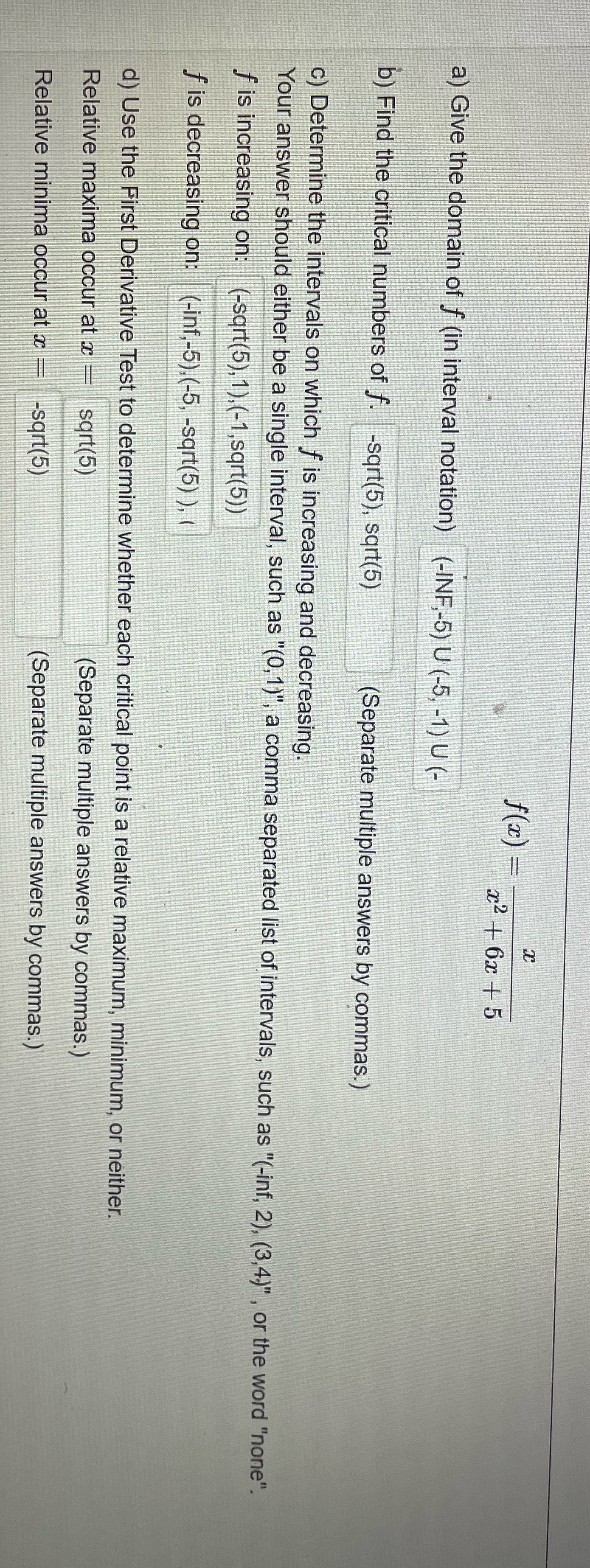
8 f(x) - x2 + 6x + 5 a) Give the domain of f (in interval notation) (-INF,-5) U (-5, -1) U (- b) Find the critical numbers of f. -sqrt(5), sqrt(5) (Separate multiple answers by commas.) c) Determine the intervals on which f is increasing and decreasing. Your answer should either be a single interval, such as "(0,1)", a comma separated list of intervals, such as "(-inf, 2), (3,4)" , or the word "none". f is increasing on: (-sqrt(5), 1), (-1, sqrt(5)) f is decreasing on: (-inf,-5),(-5, -sqrt(5) ), ( d) Use the First Derivative Test to determine whether each critical point is a relative maximum, minimum, or neither. Relative maxima occur at x sqrt(5) (Separate multiple answers by commas. ) Relative minima occur at x - -sqrt(5) (Separate multiple answers by commas. )