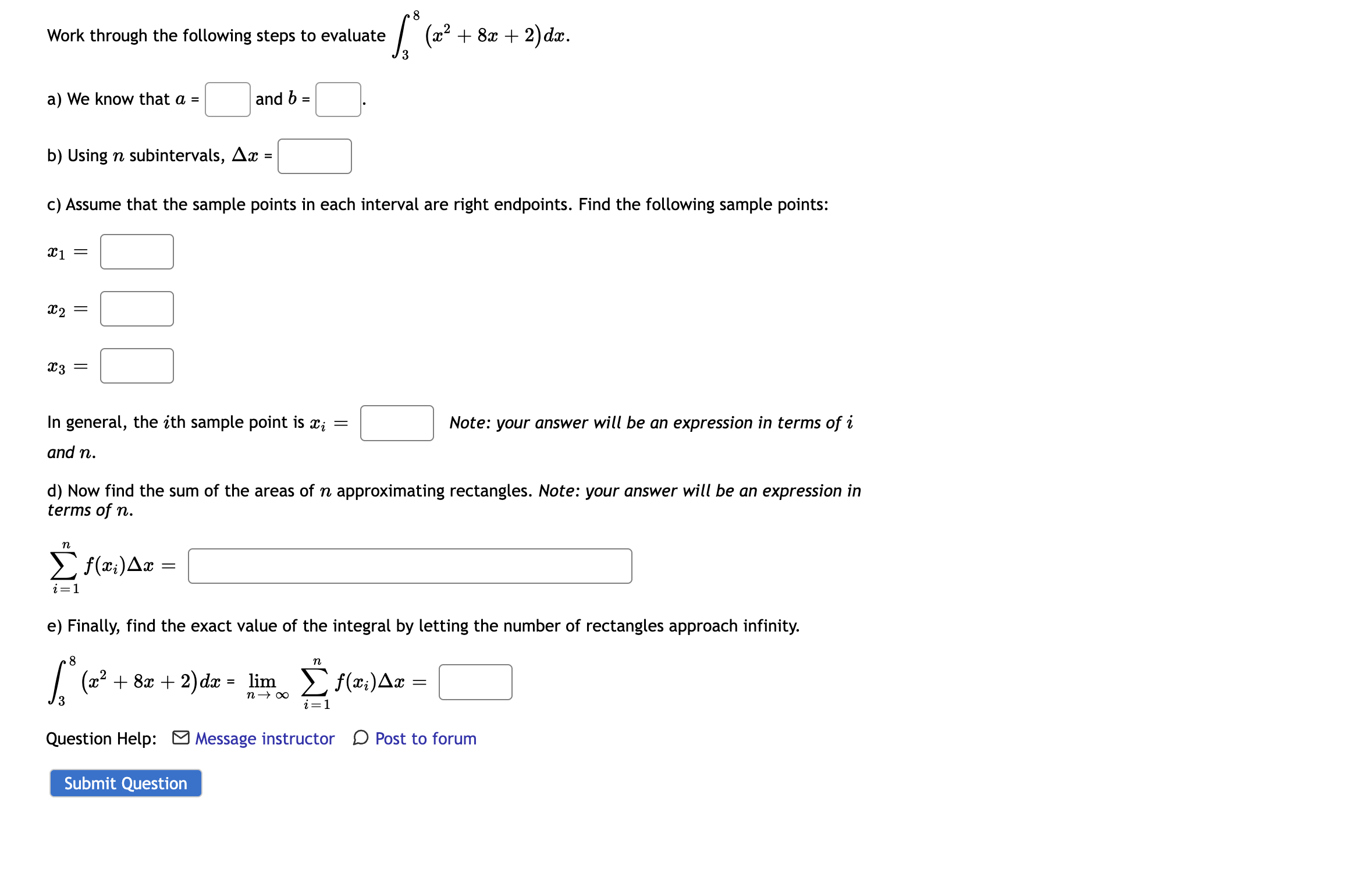
Question: 8 Work through the following steps to evaluate / (a:2 + 89: + 2)da:. 3 a) We know that a = [j and b =

![b = [3. b) Using n subintervals, A2: = [:] c) Assume](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6679c3fb101ef_0586679c3faef8fb.jpg)

![point is mi = [:] Note: your answer will be an expression](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6679c3fc906c6_0606679c3fc6441e.jpg)

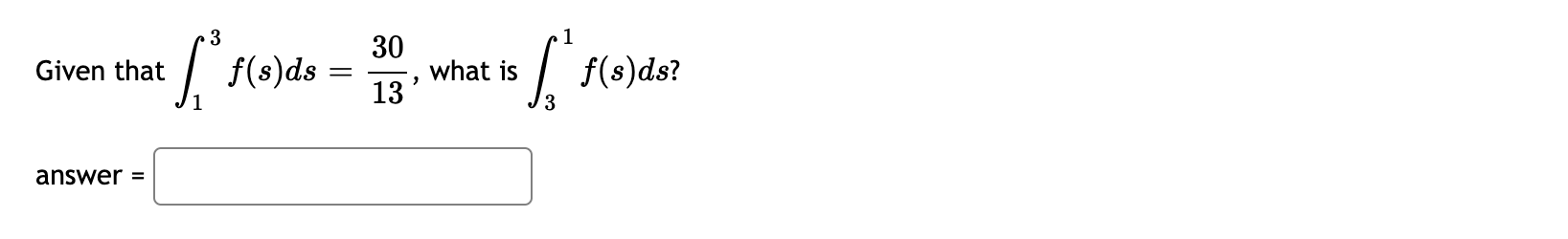
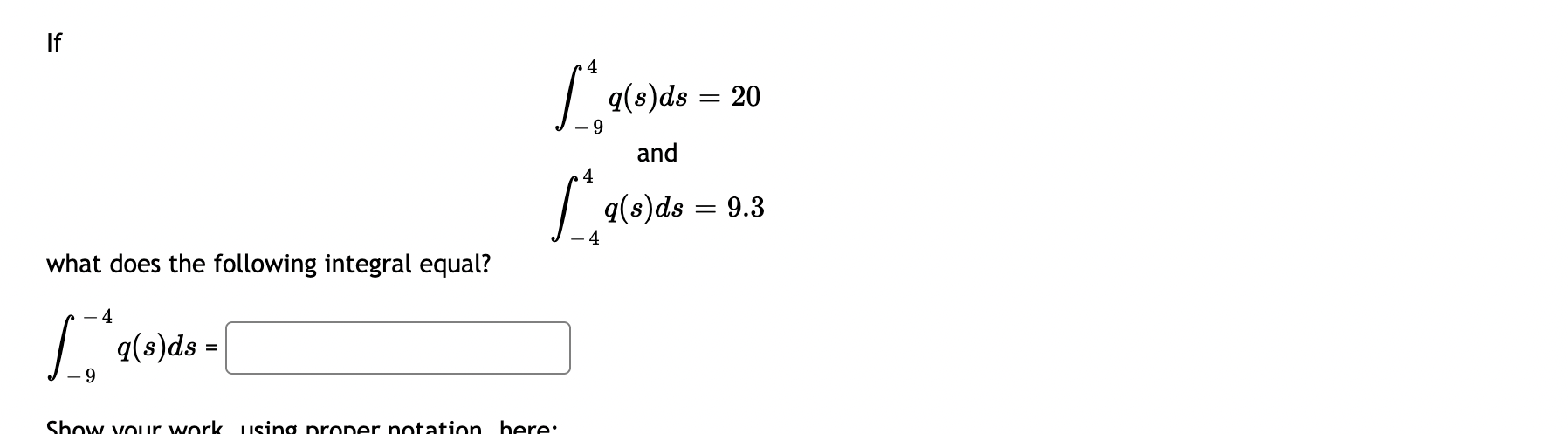

![THO" gz) x C] Question Help: El Message instructor D Post to](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6679c4000519f_0636679c3ffc4e86.jpg)
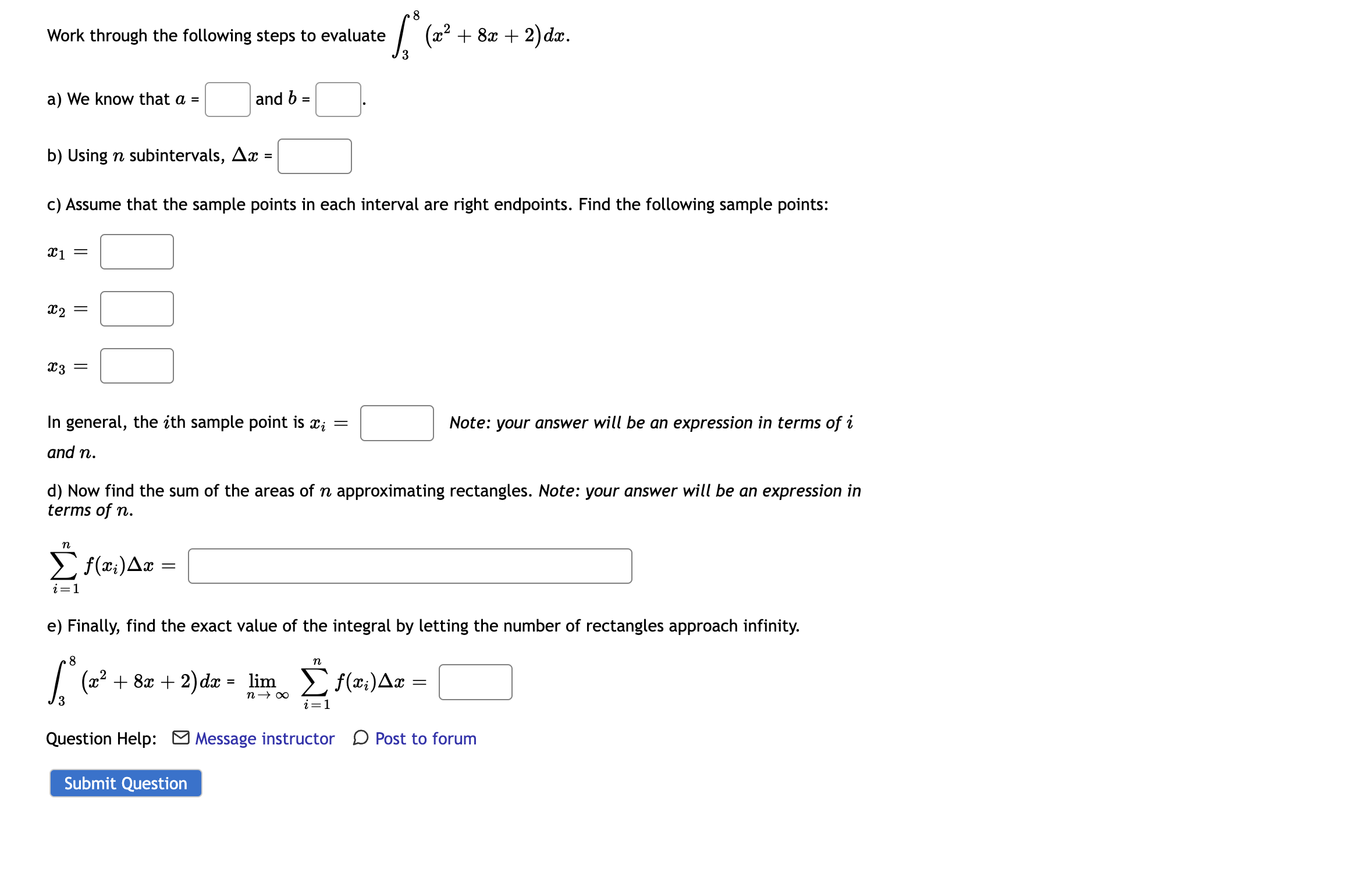
8 Work through the following steps to evaluate / (a:2 + 89: + 2)da:. 3 a) We know that a = [j and b = [3. b) Using n subintervals, A2: = [:] c) Assume that the sample points in each interval are right endpoints. Find the following sample points: 931 m2 933 BED In general, the ith sample point is mi = [:] Note: your answer will be an expression in terms off and n. d) Now find the sum of the areas of n approximating rectangles. Note: your answer will be an expression in terms of n. Z" f($i)Aw = ' i=1 e) Finally, find the exact value of the integral by letting the number of rectangles approach infinity. 8 n 2 d = lim ;A = /3(:c +8w+2)w THO" gz) x C] Question Help: El Message instructor D Post to forum Submit Question If 4 q(s)ds = 20 9 and q(s)ds = 9.3 4 what does the following integral equal? 4 q(s)ds = ShIf 28 f(x) dx = 11 - 58 and - 28 g(x) dx = 24 - 58 and - 28 h(x)dx = 25 - 58 what does the following integral equal? - 28 [7 f(x) + 59(x) - h(x)]dac = -58Work through the following steps to evaluate / (x2 + 1) dx. a) We know that a = and b = b) Using n subintervals, Ax = c) Assume that the sample points in each interval are right endpoints. Find the following sample points: C1 = C2 = 23 = In general, the ith sample point is Xi = Note: your answer will be an expression in terms of i and n. d) Now find the sum of the areas of n approximationg rectangles. Note: your answer will be an expression in terms of n. E f(xi) Ax = i= 1 e) Finally, find the exact value of the integral by letting the number of rectangles approach infinity. (x2 + 1) da = lim n -+ 0o [ f(xi)Ax = i= 1
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


