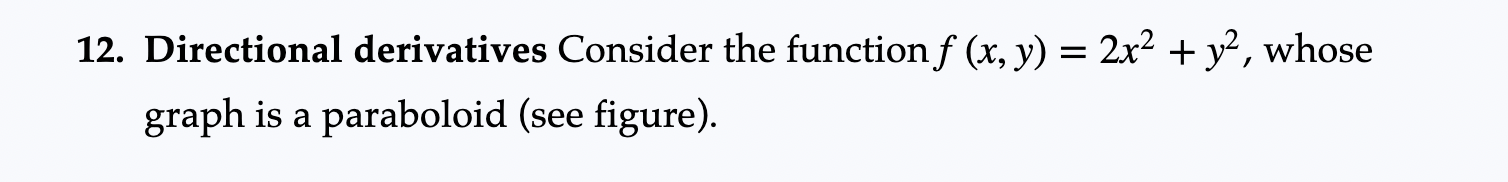
90.

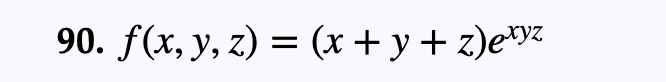
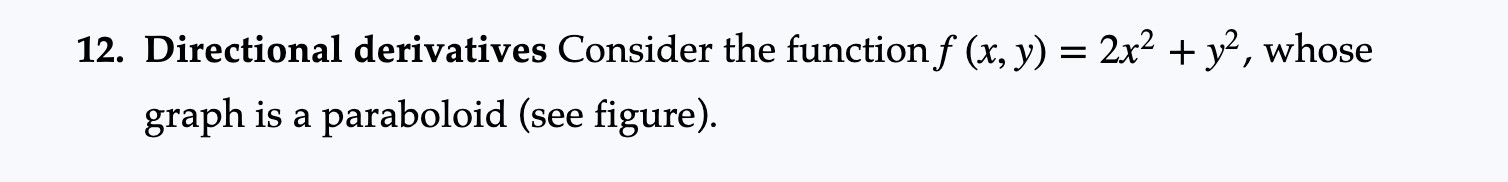
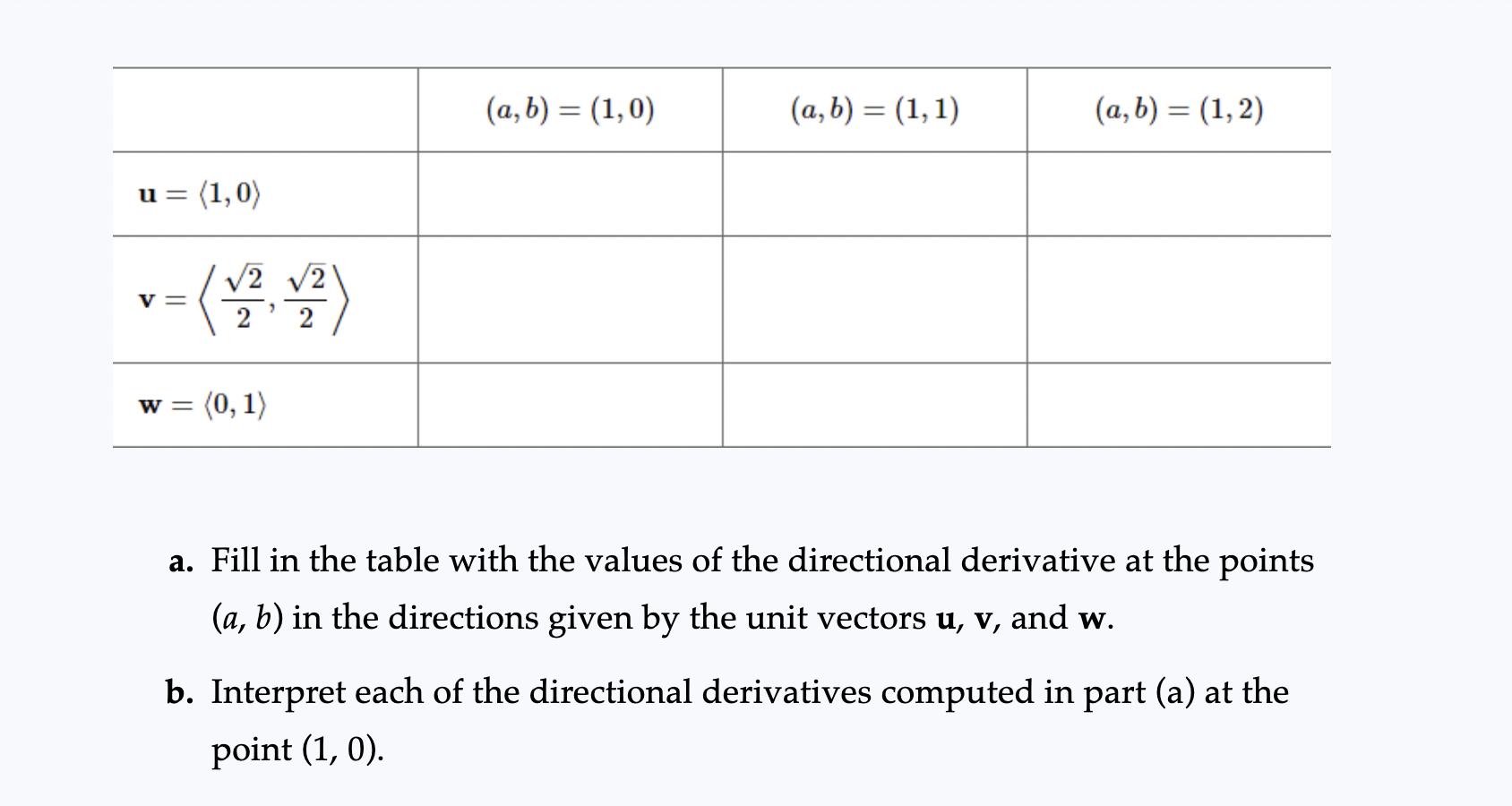
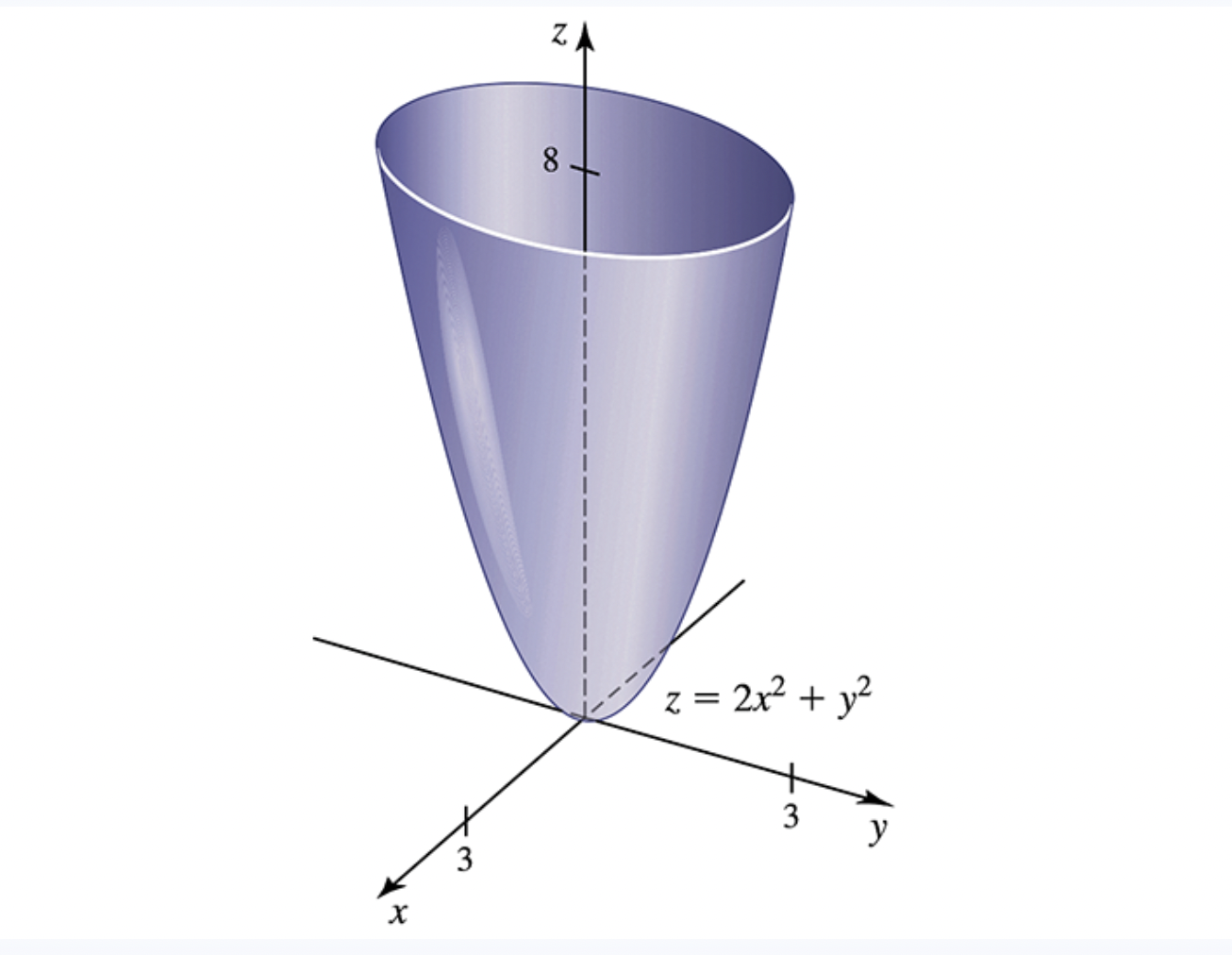
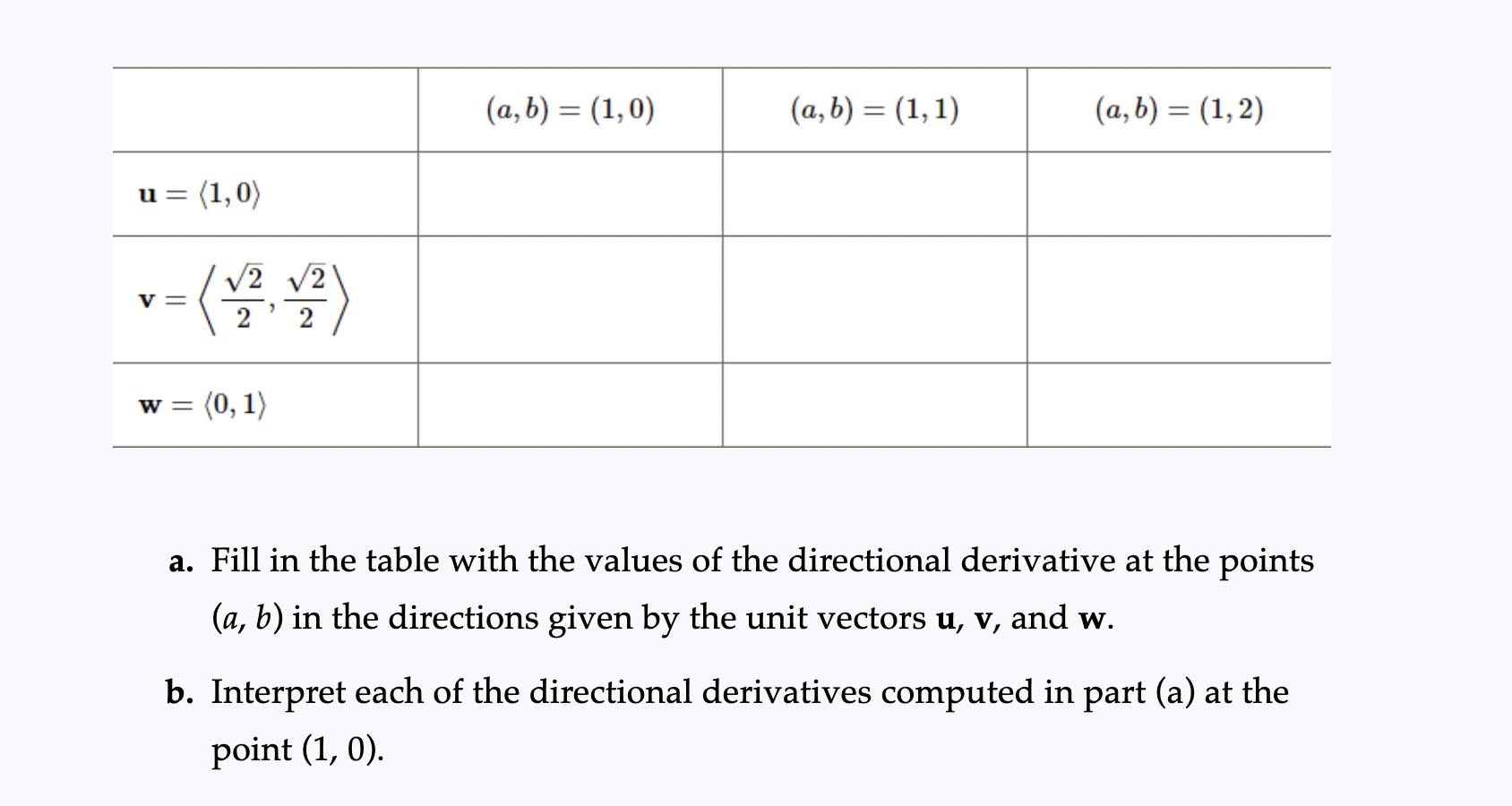
86-91. Using gradient rules Use the gradient rules of Exercise 85 to find the gradient of the following functions.90. f(x, y, Z) = (x + y + z)exyz85. Rules for gradients Use the definition of the gradient (in two or three dimensions), assume f and g are differentiable functions on R2 or R3, and let c be a constant. Prove the following gradient rules. a. Constants Rule: V(of) = cVf b. Sum Rule: V(f + g) = Vf + Vg c. Product Rule: V(fg) = (Vf)g +fVg d. Quotient Rule: V ( ) = = 82 e. Chain Rule: V(f . g) = f' (g) Vg, where f is a function of one variable12. Directional derivatives Consider the function f (x, y) = 2x2 + y2, whose graph is a paraboloid (see figure). ZA 8 - z = 2x2+ y2 y(ab) = (1:0) (0:5) = (1:1) (0:5) = (192) u: (1:02} J2 J2 w: {0.1) a. Fill in the table with the values of the directional derivative at the points (a, b) in the directions given by the unit vectors u, v, and w. b. Interpret each of the directional derivatives computed in part (a) at the point (1, 0)