Question: A. 2 The shown pulley system is connected with a block of mass ( oldsymbol{m} ). The block is released from equilibrium position with upward
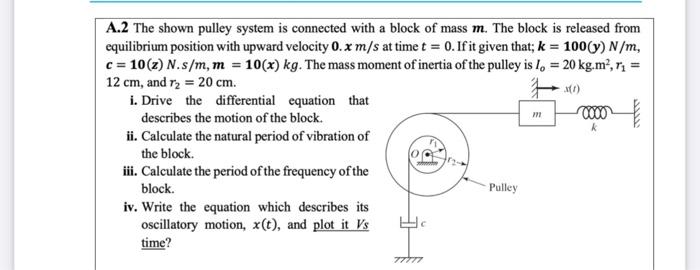
A. 2 The shown pulley system is connected with a block of mass m. The block is released from equilibrium position with upward velocity 0.xm/s at time t=0. If it given that; k=100(y)N/m, c=10(z)N.s/m,m=10(x)kg. The mass moment of inertia of the pulley is Io=20kgm2,r1= 12cm, and r2=20cm. i. Drive the differential equation that describes the motion of the block. ii. Calculate the natural period of vibration of the block. iii. Calculate the period of the frequency of the block. iv. Write the equation which describes its oscillatory motion, x(t), and plot it VS time? A. 2 The shown pulley system is connected with a block of mass m. The block is released from equilibrium position with upward velocity 0.xm/s at time t=0. If it given that; k=100(y)N/m, c=10(z)N.s/m,m=10(x)kg. The mass moment of inertia of the pulley is Io=20kgm2,r1= 12cm, and r2=20cm. i. Drive the differential equation that describes the motion of the block. ii. Calculate the natural period of vibration of the block. iii. Calculate the period of the frequency of the block. iv. Write the equation which describes its oscillatory motion, x(t), and plot it VS time
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


