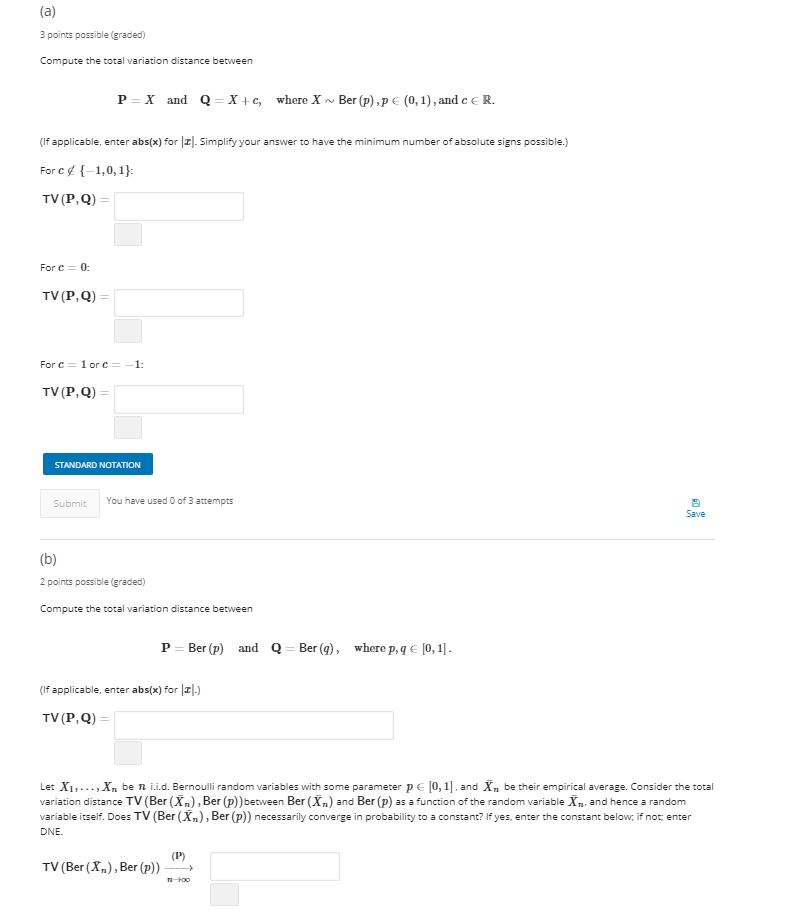
(a) 3 points possible (graded) Compute the total variation distance between P=X and Q=X+, where XBer (p),p (0,1), and CER. (If applicable, enter abs(x) for (2]. Simplify your answer to have the minimum number of absolute signs possible.) For c{-1,0,1): TV(P,Q) Forc=0 TV (P,Q) For c= 1 or c= 1: TV(P,Q) = STANDARD NOTATION Submit You have used 0 of 3 attempts Save (b) 2 points possible (graded) Compute the total variation distance between P = Ber(P) and Q Ber(q), where p, qe [0,1]. (if applicable, enter abs(x) for 13].) TV(P,Q) Let X1,...,X, ben i.i.d. Bernoulli random variables with some parameter p (0,1), and X, be their empirical average. Consider the total variation distance TV (Bern), Ber(P)) between Ber (X) and Ber(P) as a function of the random variable X, and hence a random variable itself. Does TV (Ber(X.), Ber(P)) necessarily converge in probability to a constant? If yes, enter the constant below, if not enter DNE. (P) TV(Ber (X...), Ber(P)) (a) 3 points possible (graded) Compute the total variation distance between P=X and Q=X+, where XBer (p),p (0,1), and CER. (If applicable, enter abs(x) for (2]. Simplify your answer to have the minimum number of absolute signs possible.) For c{-1,0,1): TV(P,Q) Forc=0 TV (P,Q) For c= 1 or c= 1: TV(P,Q) = STANDARD NOTATION Submit You have used 0 of 3 attempts Save (b) 2 points possible (graded) Compute the total variation distance between P = Ber(P) and Q Ber(q), where p, qe [0,1]. (if applicable, enter abs(x) for 13].) TV(P,Q) Let X1,...,X, ben i.i.d. Bernoulli random variables with some parameter p (0,1), and X, be their empirical average. Consider the total variation distance TV (Bern), Ber(P)) between Ber (X) and Ber(P) as a function of the random variable X, and hence a random variable itself. Does TV (Ber(X.), Ber(P)) necessarily converge in probability to a constant? If yes, enter the constant below, if not enter DNE. (P) TV(Ber (X...), Ber(P))