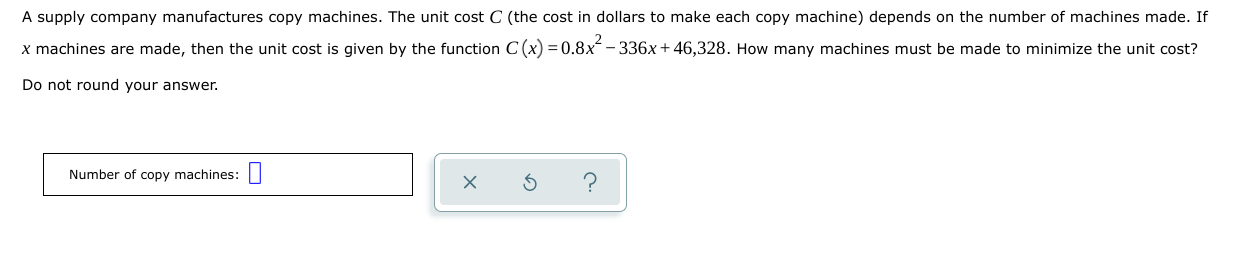
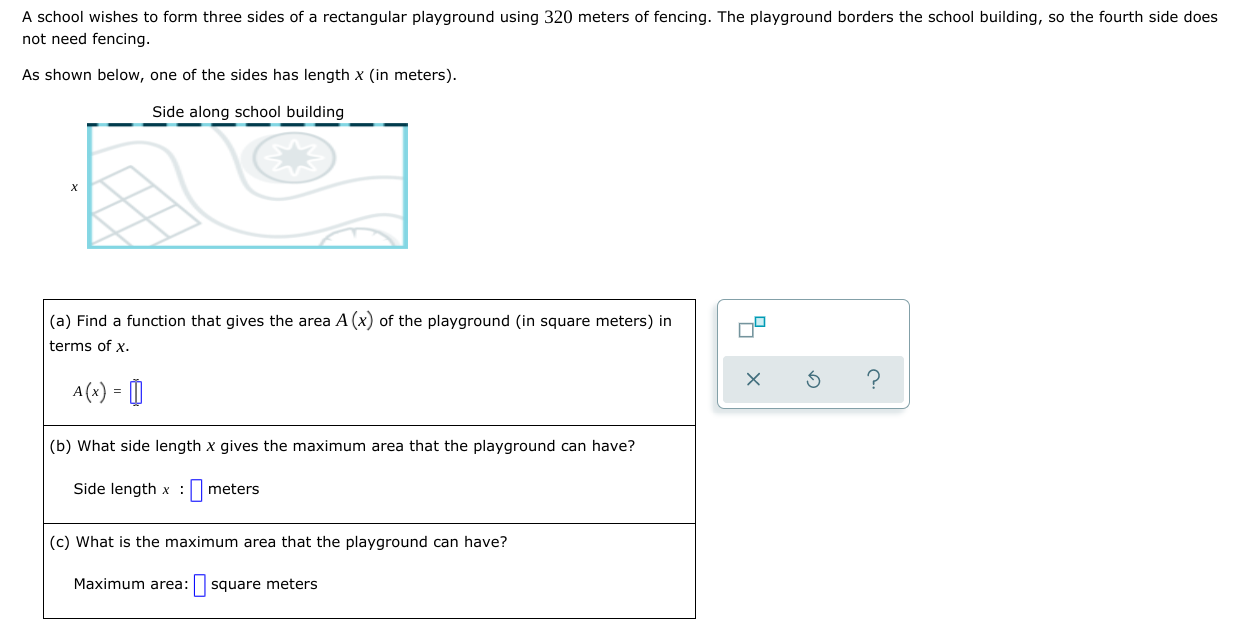
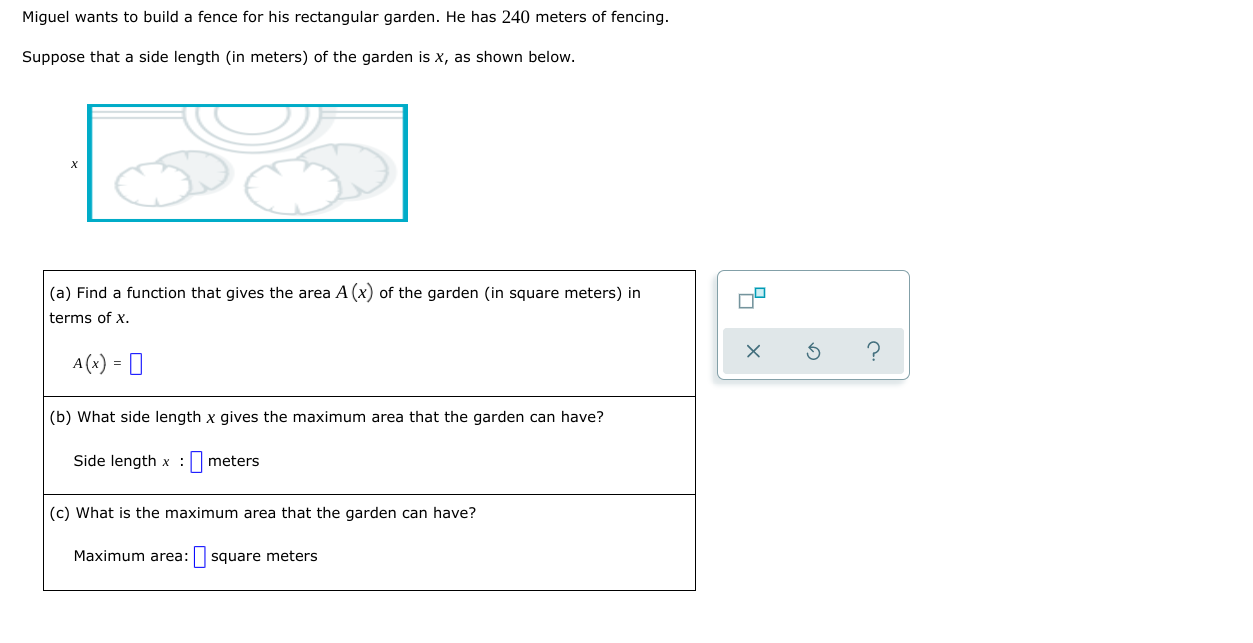
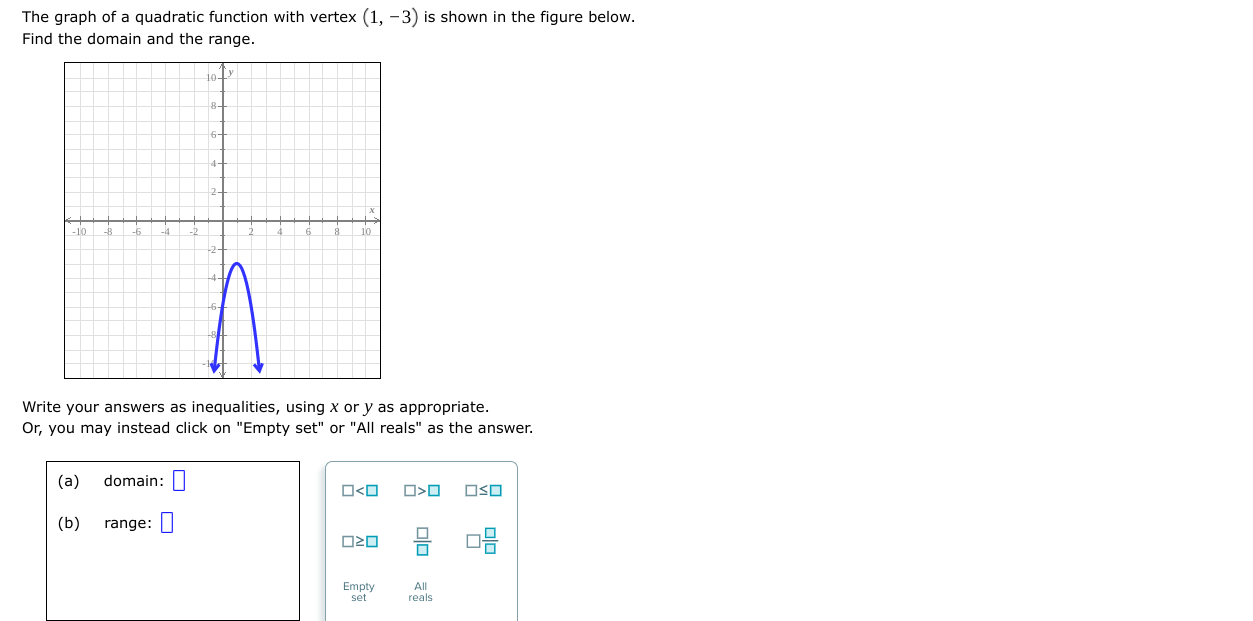
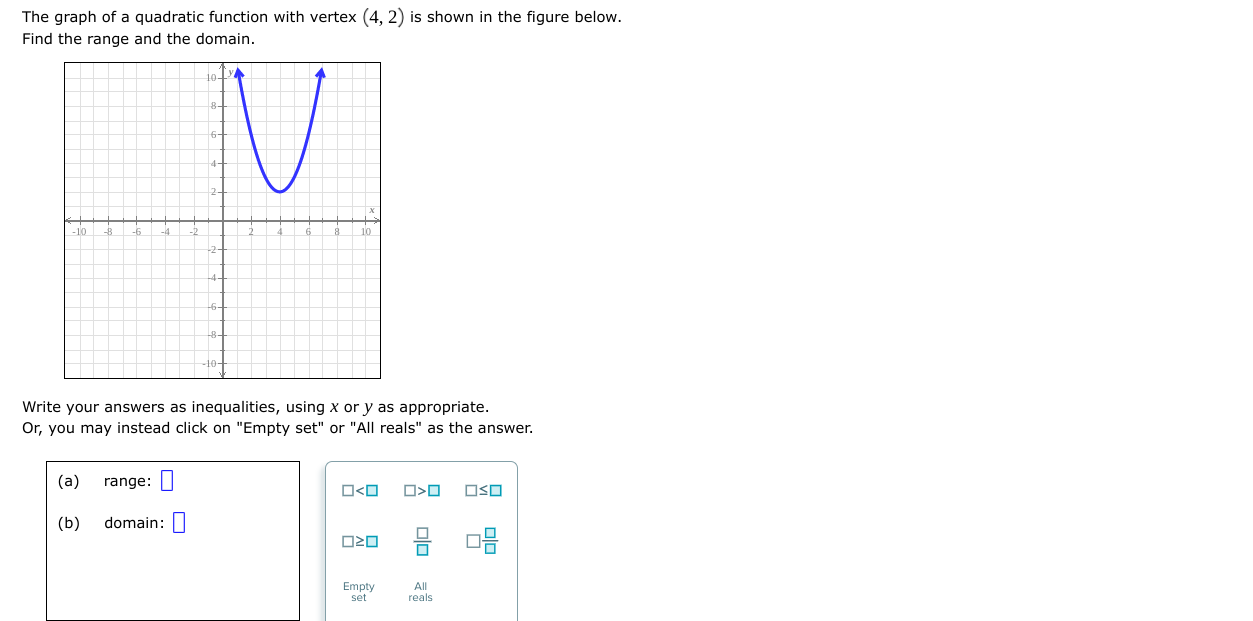
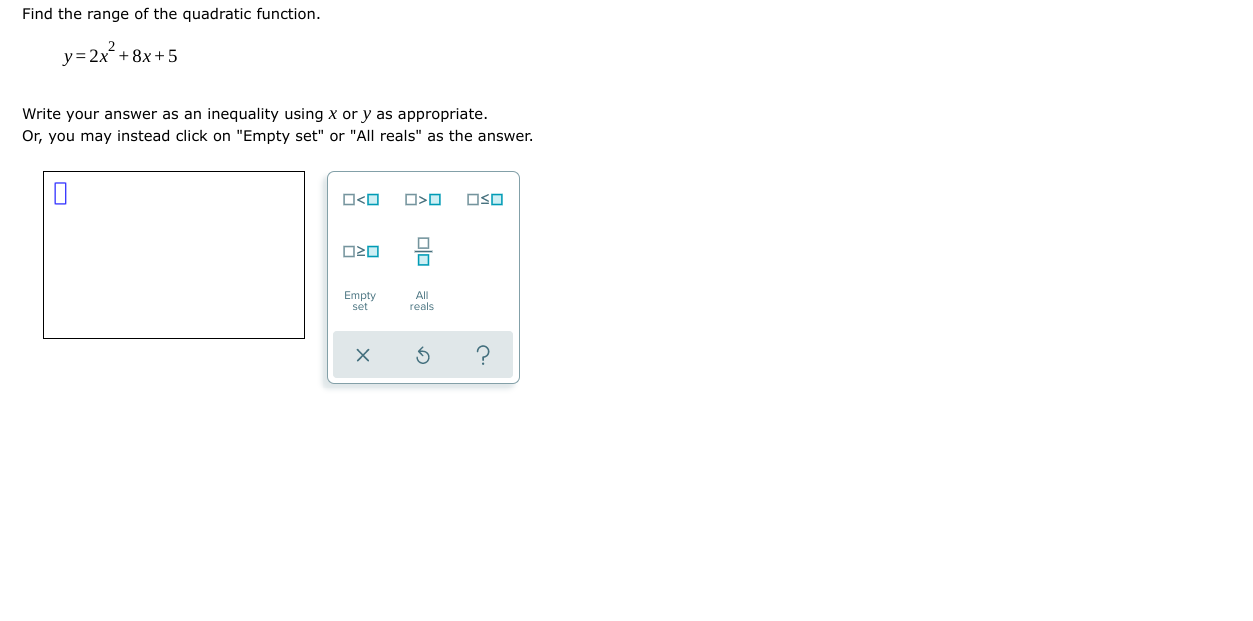
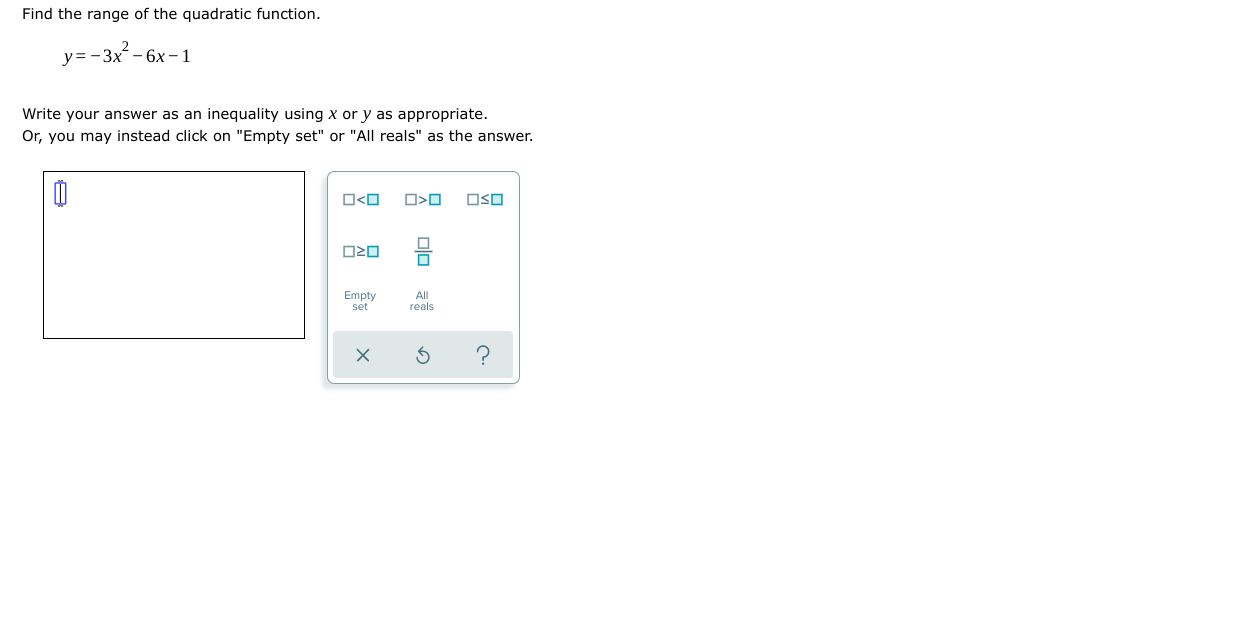
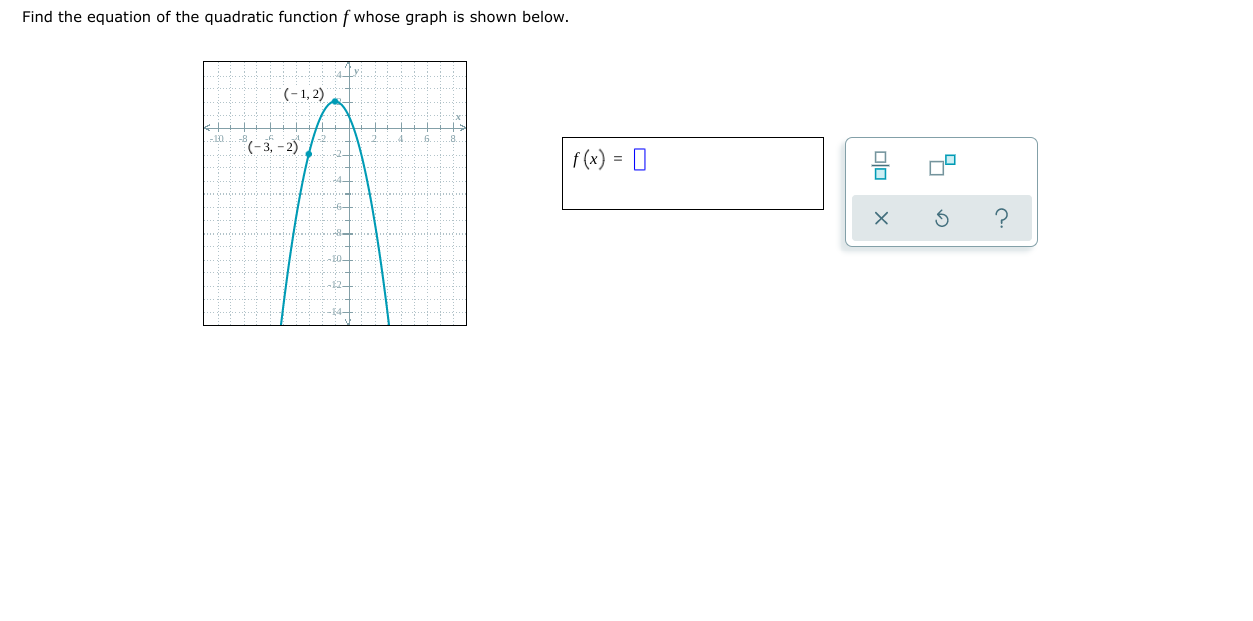
A ball is thrown vertically upward. After tseconds, its height h (in feet) is given by the function h(I)=108t 15I2. What is the maximum height that the ball will reach? Do not round your answer. Height: [I {GEL X 5 I) A suppiy company manufactures copy machines. The unit cost C (the cost in dollars to make each copy machine) depends on the number of machines made. If x machines are madeJr then the unit cost is given by the function C (X) = 0.8x2-336x+46,323. How many machines must be made to minimize the unit cost? Do not round your answer. Number of copy machines: D x \\(D Q A school wishes to form three sides of a rectangular playground using 320 meters of fencing. The playground borders the school building, so the fourth side does not need fencing. As shown below, one of the sides has length x (in meters). Side along school building (3) Find a function that gives the area A(X) of the playground (in square meters} in terms of X. A(x) =|I| (b) What side length X gives the maximum area that the playground can have? Side length x : I] meters (c) What is the maximum area that the playground can have? Maximum area: [I square meters Miguel wants to build a fence for his rectangular garden. He has 240 meters of fencing. Suppose that a side length (in meters) of the garden is X, as shown below. (a) Find a function that gives the area Apt) af the garden (in square meters) in terms of X. A(X)= I] (b) What side length x gives the maximum area that the garden can have? Side length x : E meters (c) What is the maximum area that the garden can have? Maximum area: :I square meters The graph of a quadratic function with vertex (1, -3) is shown in the figure below. Find the domain and the range. 8- 6- 4- 10 8 6 10 Write your answers as inequalities, using x or y as appropriate. Or, you may instead click on "Empty set" or "All reals" as the answer. (a) domain: 0O OSO (b) range: 020 Empty All set realsThe graph of a quadratic function with vertex (4, 2) is shown in the gure below. Find the range and the domain. Write your answers as inequalities, using X cry as appropriate. Or, you may instead click on "Empty set\" or "All reals" as the answer. (a) range: [I (b) domain: [I Find the range of the quadratic function. y=2x2+Bx+5 Write your answer as an inequality using x ory as appropriate. Or, you may instead click on "Empty set\" or "All reals" as the answer. Find the range of the quadratic function. y= 3X25X1 Write your answer as an inequality using x ory as appropriate. Or, you may instead click on "Empty set\" or "All reals" as the answer. Find the equation of the quadratic function f wn05e graph is shown below. f(x) = [I