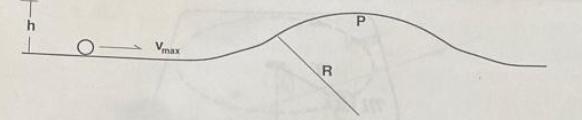
A ball rolls without slipping or sliding on a surface. The mass of the ball is given as m and the radius of the ball is given as r. The ball is made of a thin- walled metallic shell with a hollow core. The rotational inertia of the hollow ball about the central point is given as I = mr. Suppose the ball approaches a gently rolling hill as shown. Assume over the top, the hill is shaped in a circular arc with a given radius of curvature R. Assume that when the ball is at the top of the hill, it is a given height h above the level ground as shown. Assume that air resistance can be neglected. Part (a): - 20 points - Suppose we define Umar as the maximum value of the translational speed of the ball that that ensures that the ball will remain in contact with the hill as it rolls over the crest at point P above? Calculate the value Umar in terms of the given parameters. Explain how you determined this. Hint: This is "compound problem". To solve it you need to break the problem into two or more steps and solve each step. Part (b): 5 points - Conceptual question: Suppose I change the problem so that the ball is now solid uniform sphere instead of a hollow shell. Otherwise the ball has the same mass and the same radius. How does this change your answer for part (a). Does the the value of Umar increase, decrease, or stay the same relative to your calculation for Part (a)? - h 1 Vmax R la P