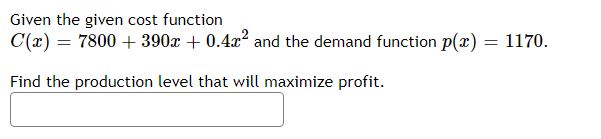
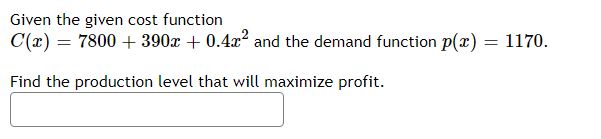
A box with a square base and open too must have a volume of 143?48 m3. We wish to find the dimensions of the box that minimize the amount of material used. First, find a formula for the surface area of the box in terms of only as, the Length of one side of the square base. [Hint: use the volume formula to express the height of the box in terms of 22.] Simplify your formula as much as possible. AG\") = i i Next, find the derivative, A(:t:). A'tm) = i i Now, calculate when the derivative equals zero, that is, when 44(3) 2 i]. [Hint: multiply both sides by $2 .1 .4132) = Uwhen a: =| We next have to make sure that this value of 3 gives a minimum value for the surface area. Let's use the second derivative test. Find A".(:E) mm) = i | Evaluate A"(:l:) at the atvalue you gave above. Given the given cost function C(13) = 7800 + 3901', + 0.49:2 and the demand function p(:t:) : 1170. Find the production level that will maximize profit. For the given cost function C(23) = 57600 + 200:1; + 32, First, find the average cost function. Use it to find: a} The production level that will minimize the average cost \"l l b] The minimal average cost El ,l