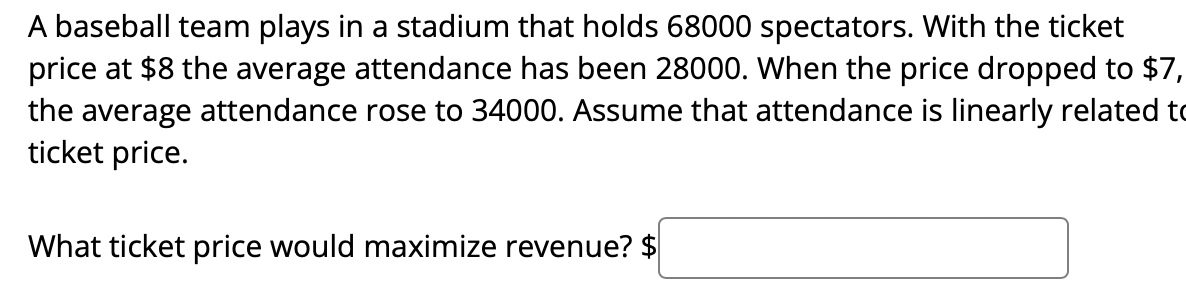
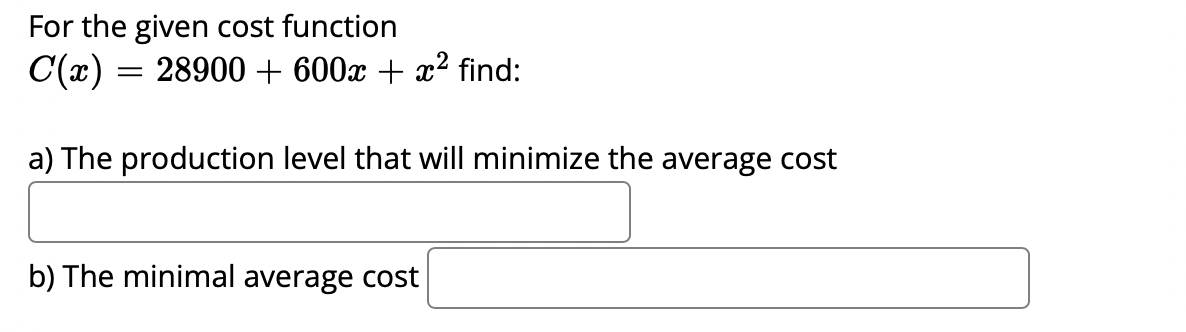
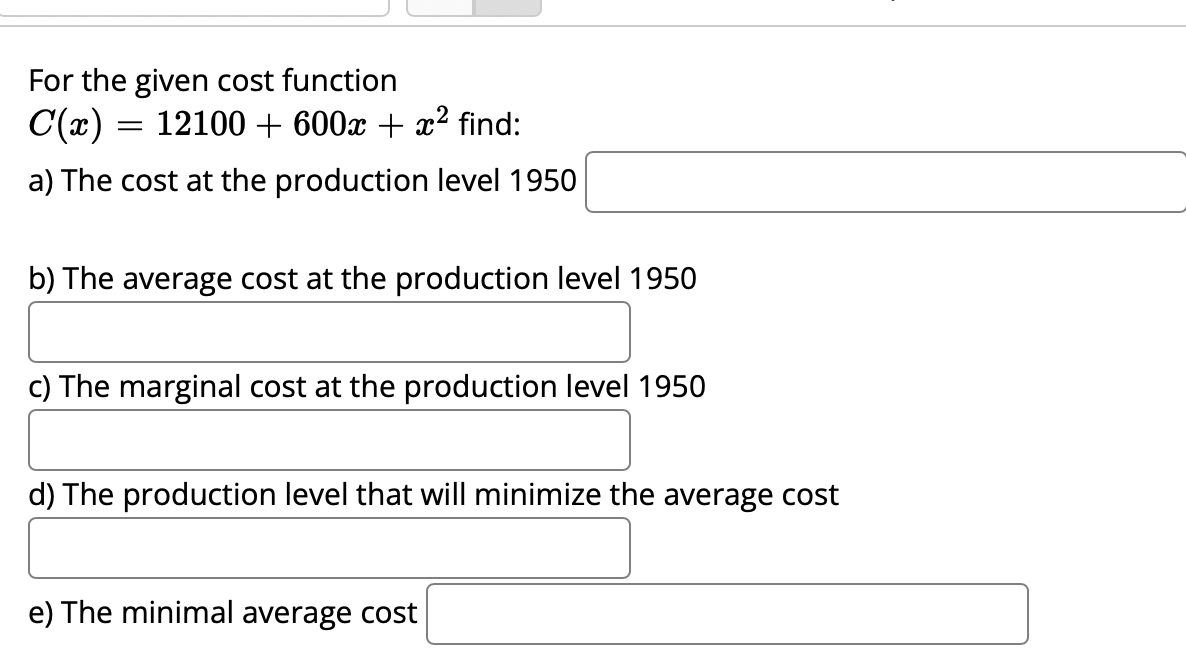
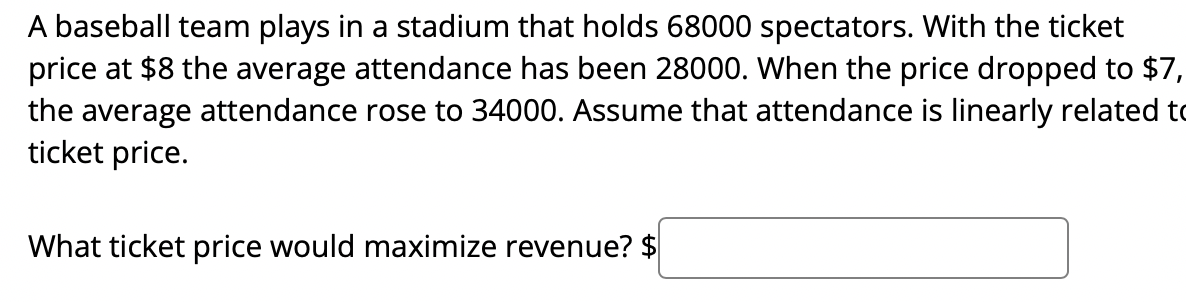
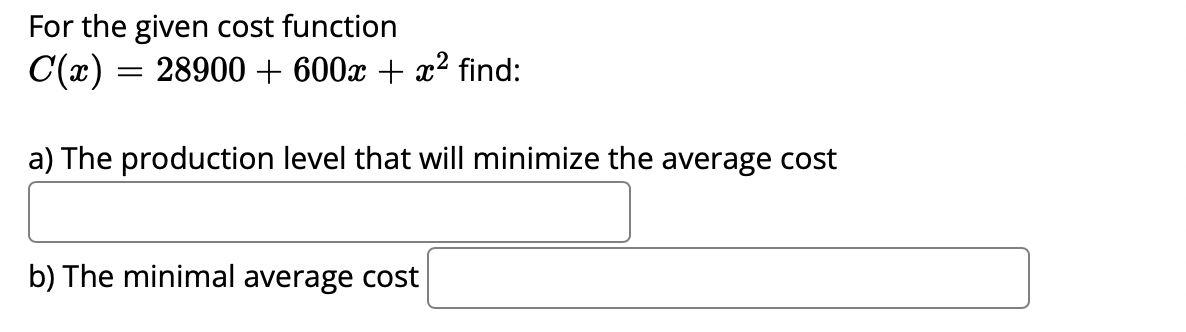
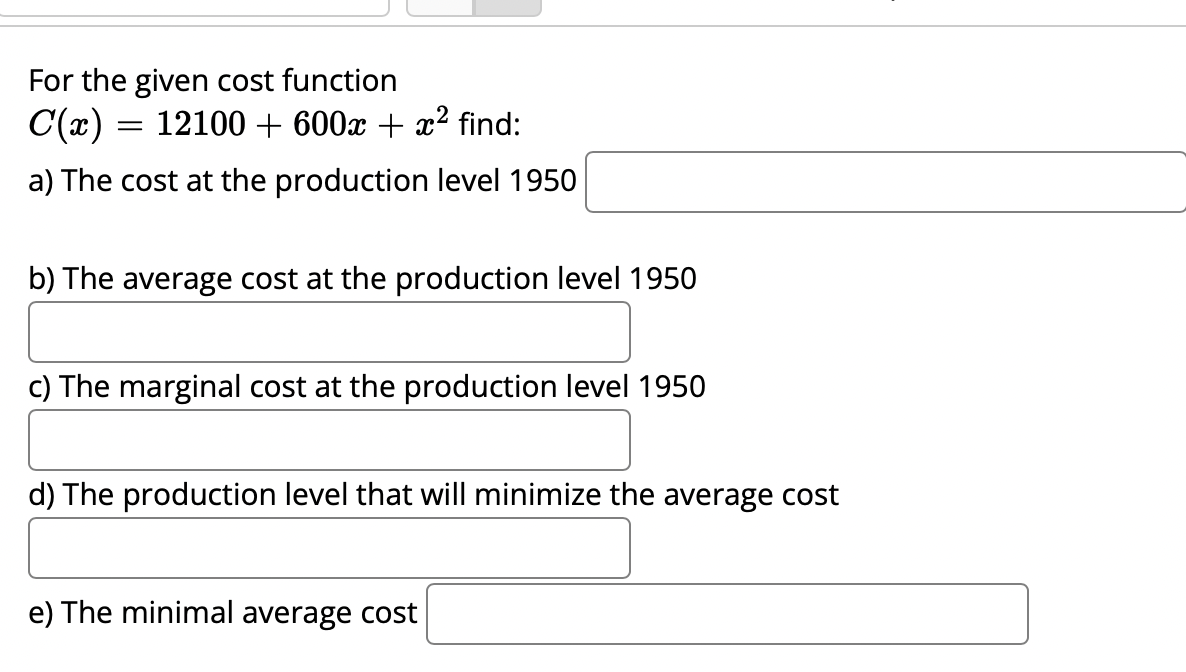
A box with a square base and open top must have a volume of 42592 (21113. We wist to find the dimensions of the box that minimize the amount of material used. First, find a formula for the surface area of the box in terms of only :3, the length of one side of the square base. [Hintz use the volume formula to express the height of the box in terms ofm.] Simplify your formula as much as possible. AW = :1 Next, nd the derivative, A ' (m). me: Now, calculate when the derivative equals zero, that is, when A ' (3:) = 0. [Hint: multiply both sides by $2.] A'(:1:) = 0whenm = We next have to make sure that this value ofm gives a minimum value for the surface area. Let's use the second derivative test. Find A".(:L') .1.) = S Evaluate A"(:v) at the m-value you gave above. For the given cost function 0(3) 2 12100 + 600:1: + 3:2 find: a) The cost at the production level 1950' b) The average cost at the production level 1950 Z c) The marginal cost at the production level 1950 Z d) The production level that will minimize the average cost Given the given cost function 0(3) 2 4650 + 580:1: + 1.93:2 and the demand function 13(3) 2 1740. Find the production level that will maximaze profit. S A baseball team plays in a stadium that holds 68000 spectators. With the ticket price at $8 the average attendance has been 28000. When the price dropped to $7, the average attendance rose to 34000. Assume that attendance is linearly related t