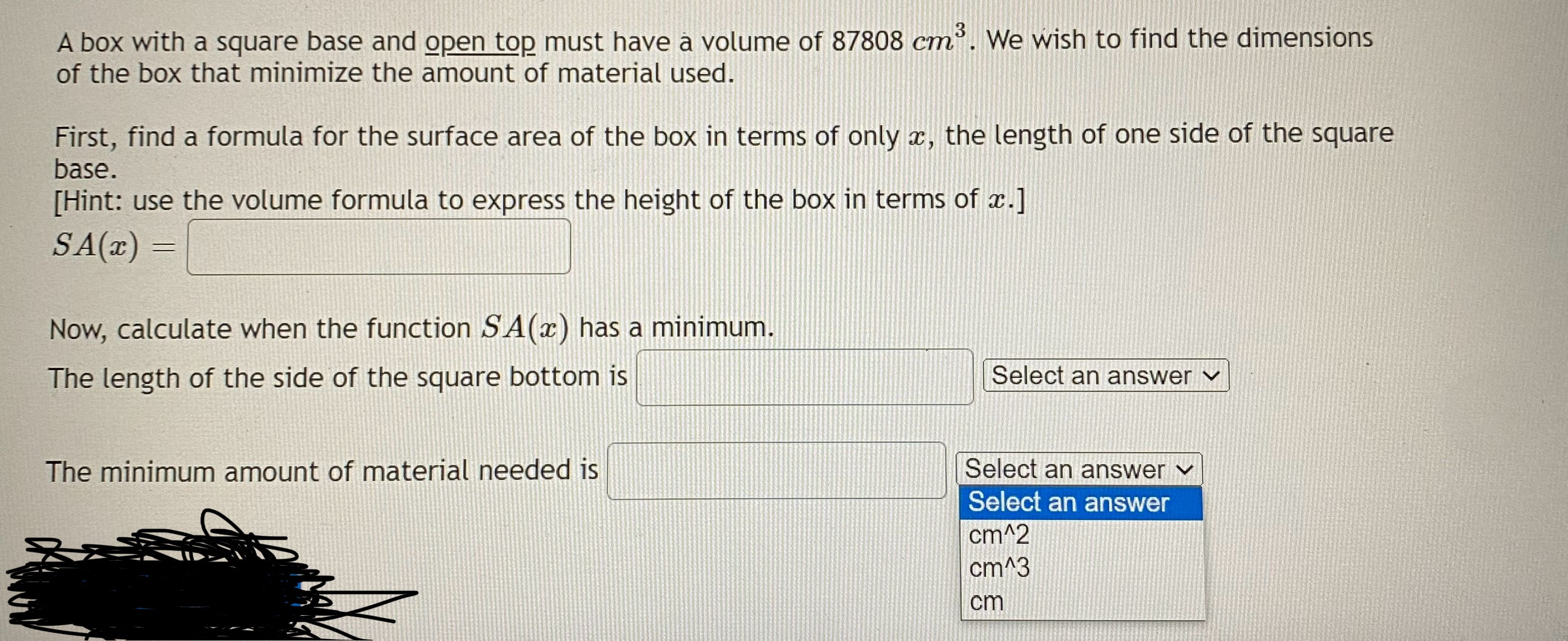
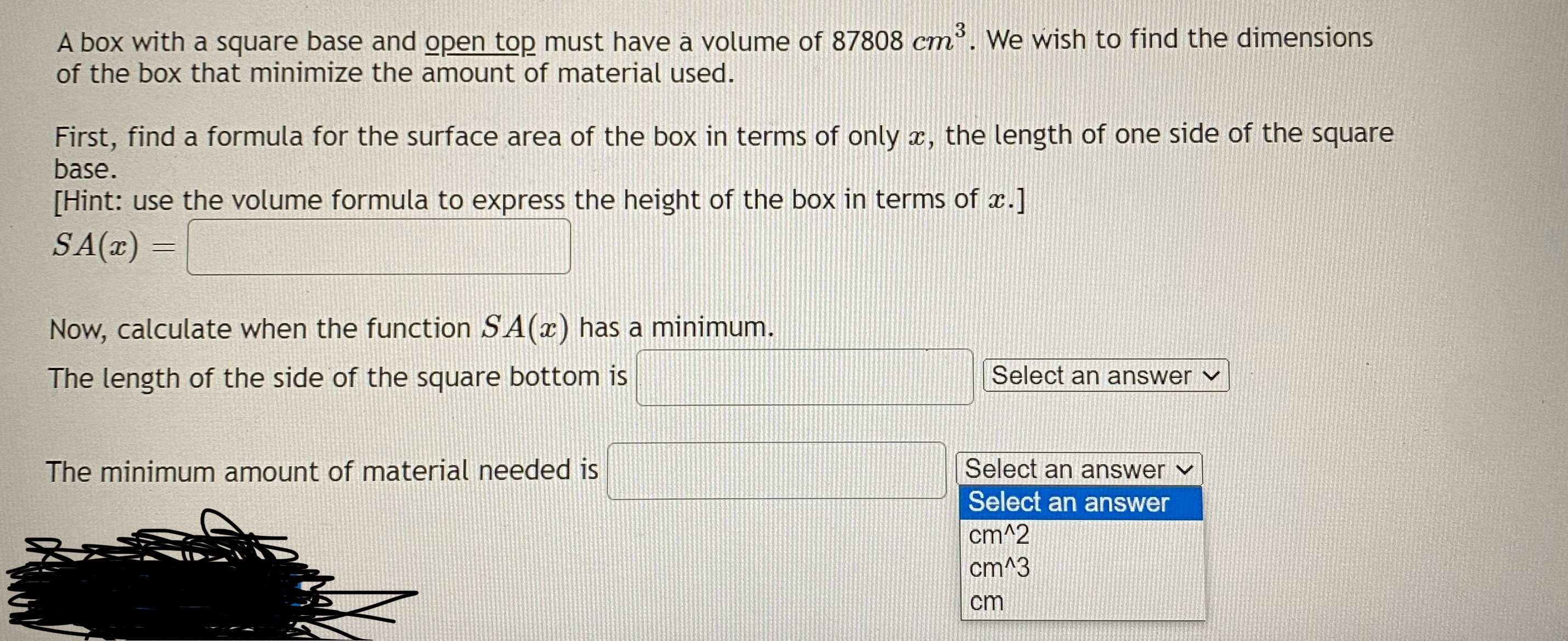
Question: A box with a square base and open top must have a volume of 87808 cm. We wish to find the dimensions of the box


![of ac. ] SA(x) Now, calculate when the function SA(x ) has](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666648a94fec2_305666648a92f4f2.jpg)
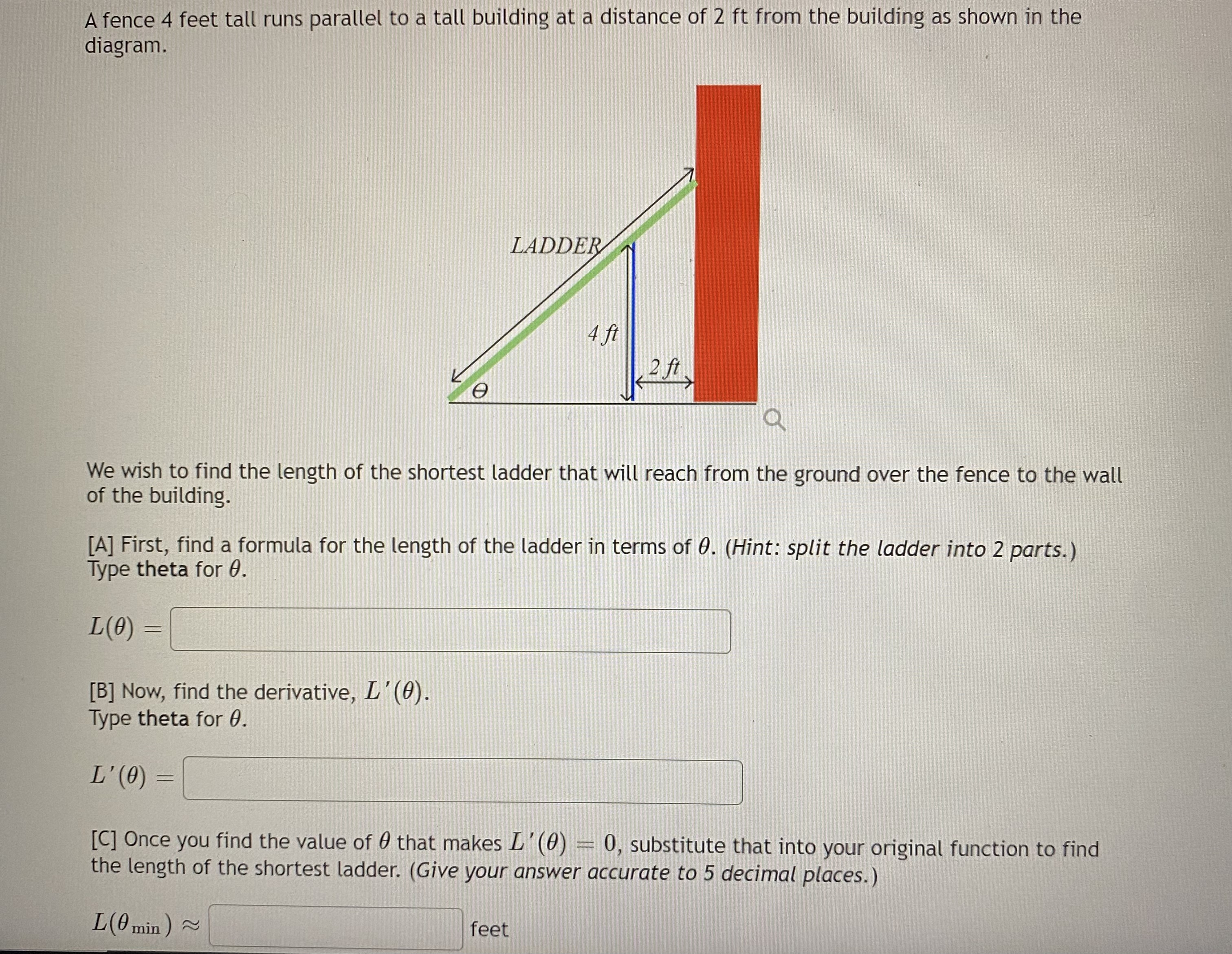
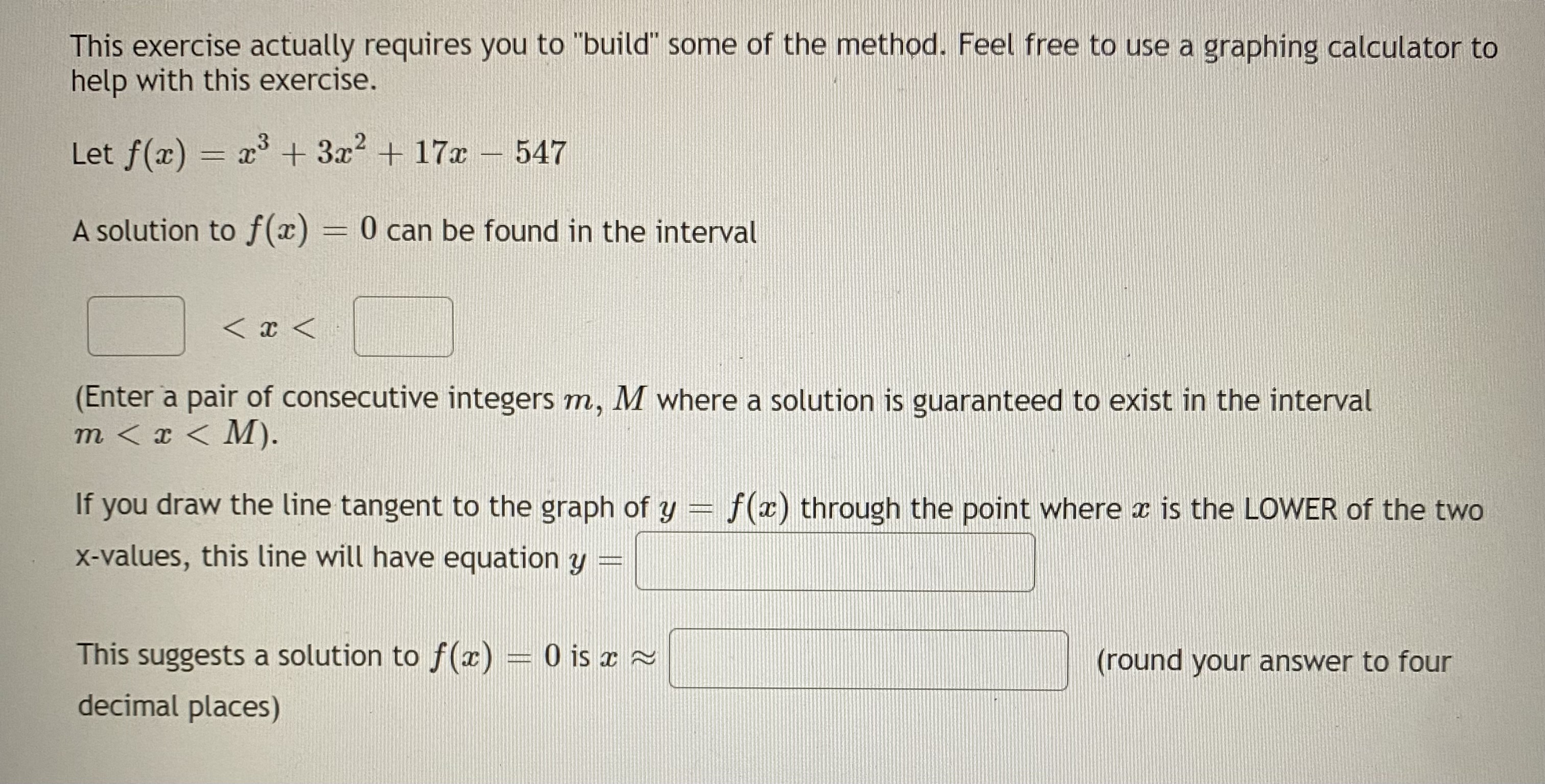

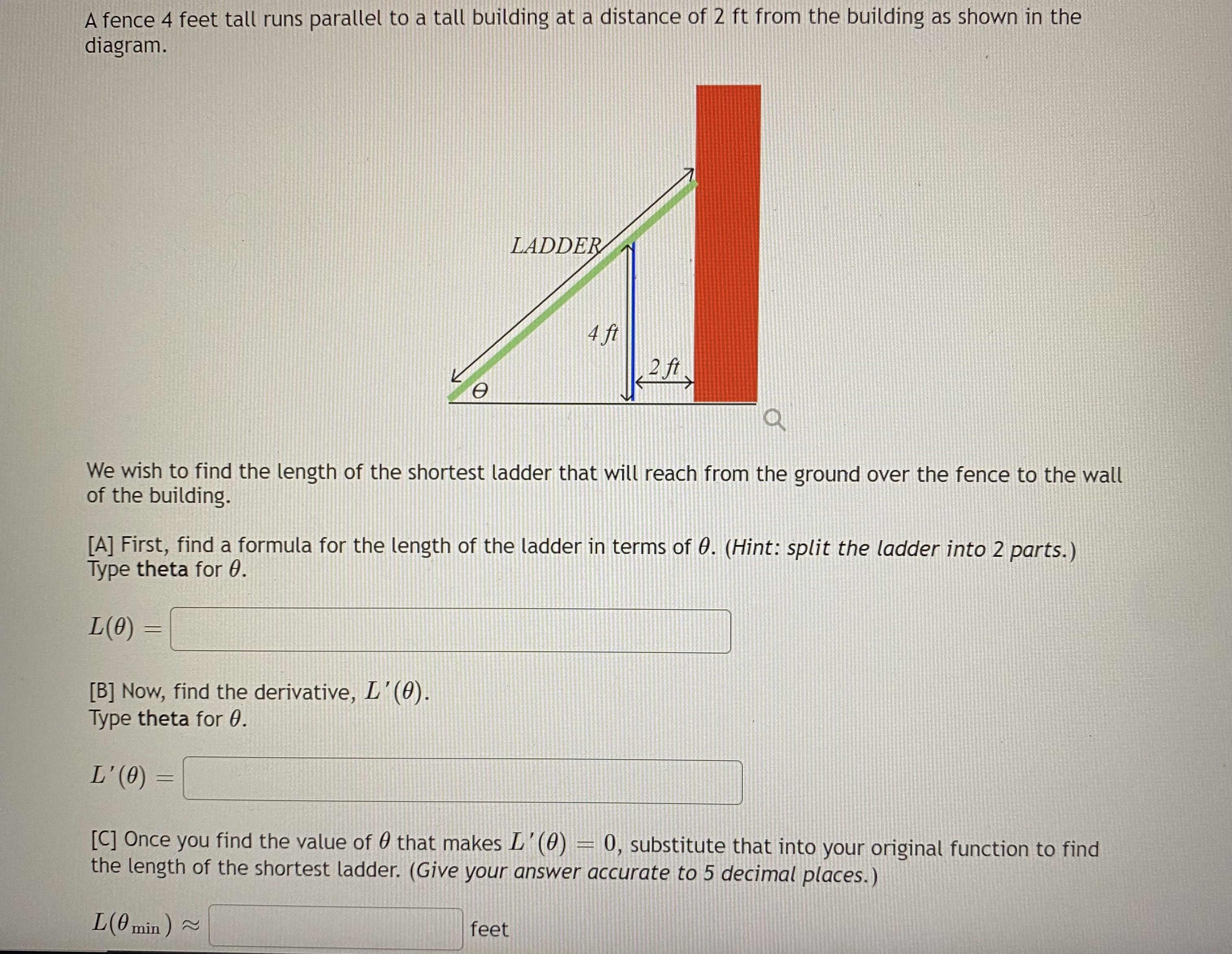
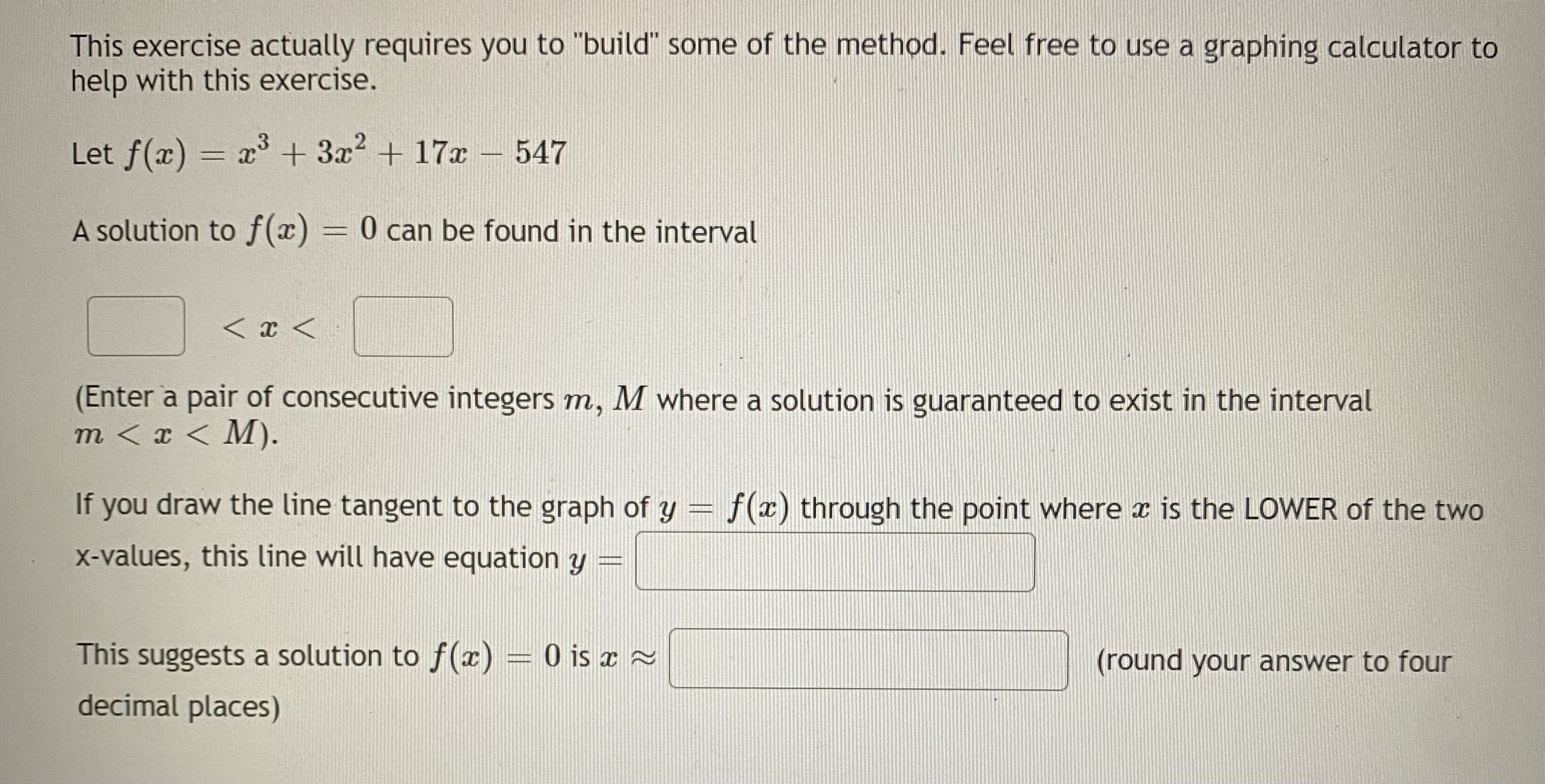
A box with a square base and open top must have a volume of 87808 cm. We wish to find the dimensions of the box that minimize the amount of material used. First, find a formula for the surface area of the box in terms of only a, the length of one side of the square base. [Hint: use the volume formula to express the height of the box in terms of ac. ] SA(x) Now, calculate when the function SA(x ) has a minimum. The length of the side of the square bottom is Select an answer The minimum amount of material needed is Select an answer v Select an answer cm^2 cm^3 cmYou are a lifeguard and spot a distressed child 60 meters along the shore and 50 meters from the shore to the child. You run along the shore and for a while and then jump into the water and swim from there directly to child. You can run at a rate of 4 meters per second and swim at a rate of 0.9 meters per second. How far along the shore should you run before jumping into the water in order to get to the child in the least amount of time? Round your answer to three decimal places.A fence 4 feet tall runs parallel to a tall building at a distance of 2 ft from the building as shown in the diagram. LADDER Aft 2 ft e Q We wish to find the length of the shortest ladder that will reach from the ground over the fence to the wall of the building. [A] First, find a formula for the length of the ladder in terms of 0. (Hint: split the ladder into 2 parts. ) Type theta for 0. L(0 ) [B] Now, find the derivative, L'(0). Type theta for 0. L' (0) [C] Once you find the value of 0 that makes _'(0) - 0, substitute that into your original function to find the length of the shortest ladder. (Give your answer accurate to 5 decimal places.) L(0 min) ~ feetThis exercise actually requires you to "build" some of the method. Feel free to use a graphing calculator to help with this exercise. Let f(ac) = 23 + 3x2 + 17x - 547 A solution to f(x) = 0 can be found in the interval
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


