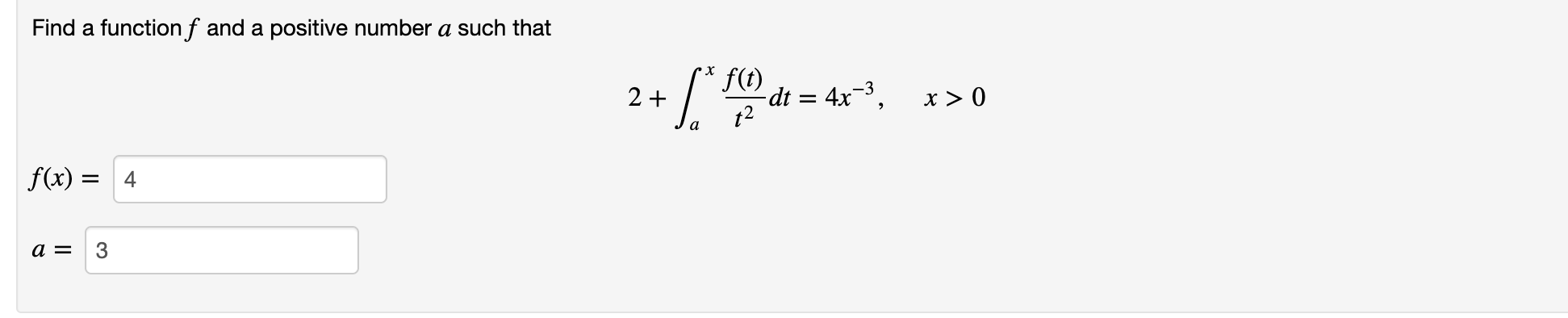
A car drives down a road in such a way that its velocity (in m/s) at time t (seconds) is v(t) = 31 1/2 Then the car's average velocity (in m/s) between t = 2 and t = 8 is equal to +5. The table gives values of a continuous function. Use the midpoint rule (n = 3) to estimate the average value of on [10,40]. x 10 15 20 25 30 35 40 f(x)21 34 4833 5462 46 Estimate = Find a function f and a positive number a such that x f(t) - dt 2+ ["dr = 4x t2 f(x) = 4 a = 3 " x > 0