A certain process in a manufacturing line that you oversee is very expensive to stop, so on average you're willing to stop it every 1 in 50,000 samples if the process is in control (in other words, you're aiming for an ARL₀ of 50,000). The standard WECO rules have ARL₀ less than 1000, so you decide to use modified versions of the rules.

3.1) If you're aiming for an ARL₀ of at least 50,000, what is the associated probability that an in-control process will set off an alarm? Answer in decimal form, e.g., for 1% you would enter "0.01", and answer to at least 5 decimal places.

3.2) The first rule you will use is that if a point is more than x from the mean, it automatically triggers an alarm. What value should you use for x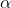? (Do not round to the nearest integer value. For example, if you calculate that the cutoff you want is 3.55 standard deviations, enter "3.55")

3.3) The second rule you will use is that if too many consecutive points are more than 1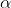 from the mean, an alarm is triggered. How many consecutive points beyond 1 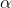should trigger an alarm? (Round up to the next integer value. For example, if you calculate that the cutoff corresponds to 7.21 consecutive points, enter "8")

3.4) The third rule you will use is that if too many consecutive points are on the same side of the mean, an alarm is triggered. How many consecutive points on the same side of the mean should trigger an alarm? (Round up to the next integer value)

3.5) If you're using the standard WECO rules in a control chart that uses a sample size of n=5, a mean shift of 0.2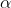 will take an average of 24 samples to trigger an alarm. In other words, for a mean shift of 0.2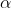, you'd have an ARL₁ of 24.

If you used the modified WECO rule from part 3.4 with a sample size of n=5, what would the ARL₁ be? (Round to the nearest integer)

3.6) If we wanted to be very careful about avoiding false alarms too often, but we wanted to avoid increasing our ARL₁ values, what course of action should we take rather than modifying the WECO rules?

Transcribed image text