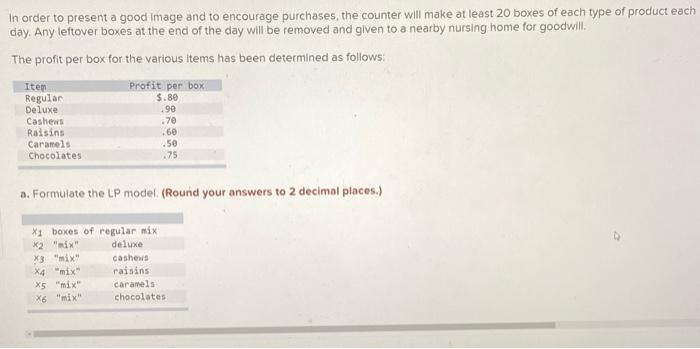
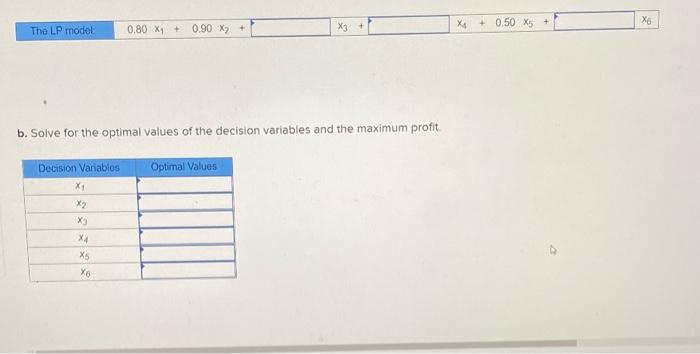
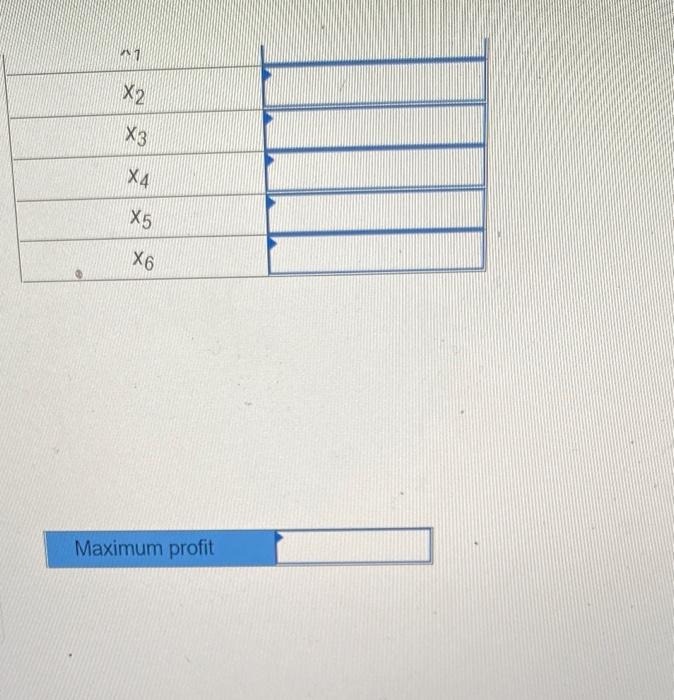
Question: A chocolate maker has contracted to operate a small candy counter in a fashionable store. To start with the selection of offerings will be intentionally

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


