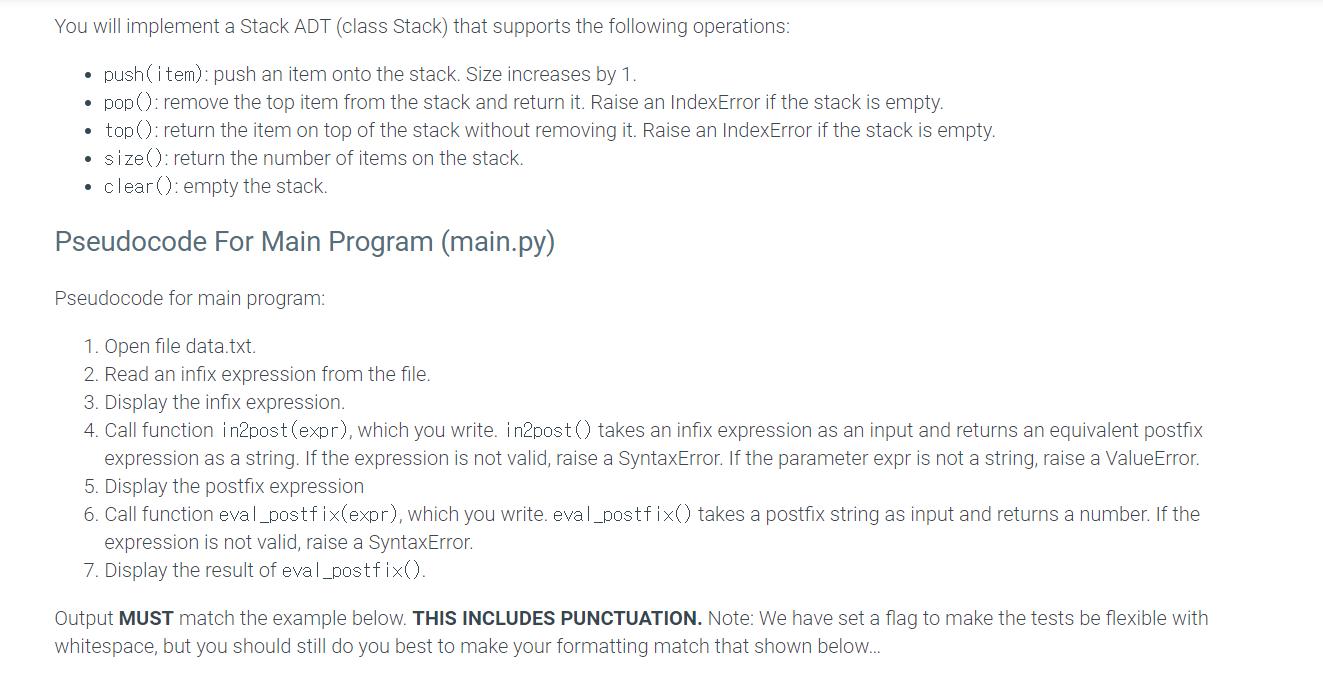
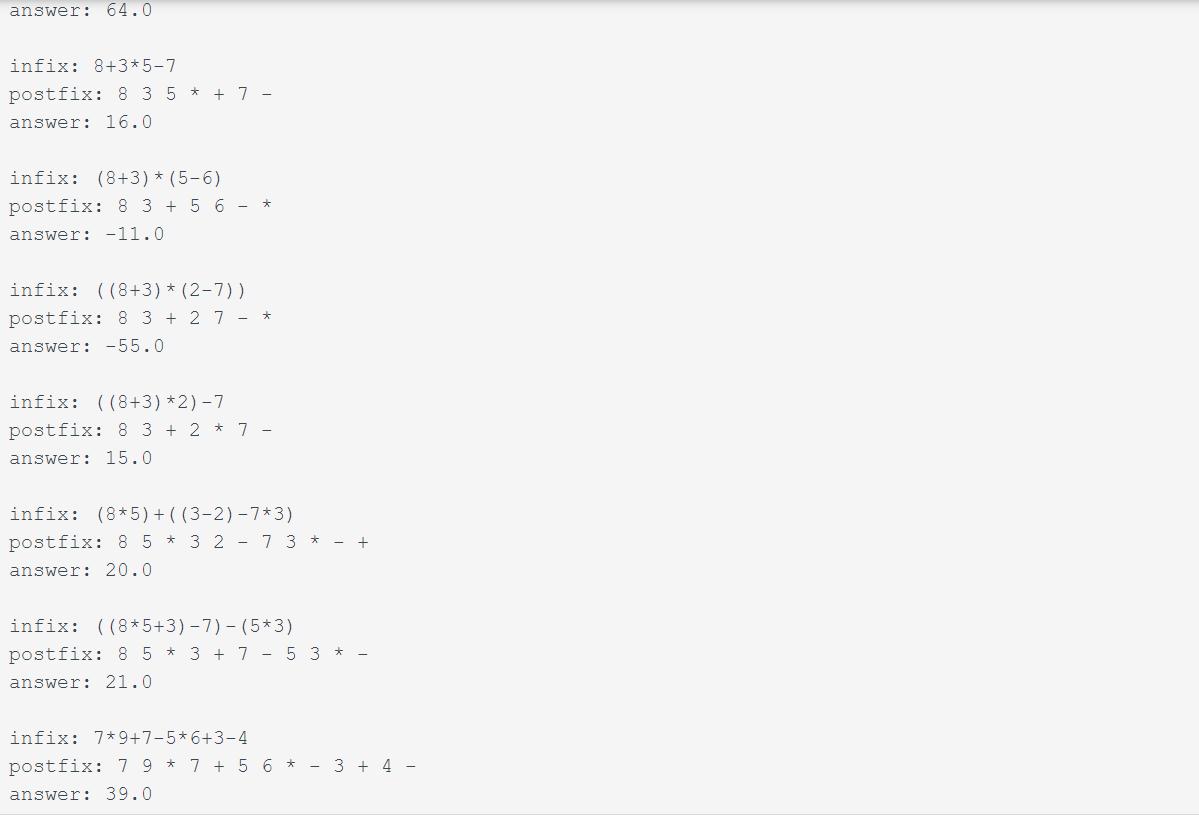
A common problem in computer science and programming is to convert information from one format into another format that is more convenient to deal with. One such classical computer science problem is to read infix mathematical expressions, convert them to postfix, and then evaluate the postfix expressions. The most common solutions involve using a stack to help with the conversion. Another common problem is to read someone else's pseudocode and implement an algorithm to match. You practice that skill with this project as well. For this project, will write your own Stack ADT, then use the stack to do the conversion based on pseudocode given below. Input will be from a text file, and output will be written to a text file. You have to write your own code to solve the problem. Your code must pass the test cases we give you WITHOUT MODIFICATION. Stack ADT (stack.py) You will implement a Stack ADT (class Stack) that supports the following operations: push(item): push an item onto the stack. Size increases by 1. pop(): remove the top item from the stack and return it. Raise an IndexError if the stack is empty. top(); return the item on top of the stack without removing it. Raise an IndexError if the stack is empty. size(); return the number of items on the stack. clear(): empty the stack. Pseudocode For Main Program (main.py) Pseudocode for main program: 1. Open file data.txt. 2. Read an infix expression from the file. 3. Display the infix expression. 4. Call function in2post (expr), which you write. in2post() takes an infix expression as an input and returns an equivalent postfix expression as a string. If the expression is not valid, raise a SyntaxError. If the parameter expr is not a string, raise a ValueError. 5. Display the postfix expression 6. Call function eval postfix(expr), which you write. eval_postfix() takes a postfix string as input and returns a number. If the expression is not valid, raise a SyntaxError. 7. Display the result of eval postfix(). Output MUST match the example below. THIS INCLUDES PUNCTUATION. Note: We have set a flag to make the tests be flexible with whitespace, but you should still do you best to make your formatting match that shown below... infix: 4 postfix: 4 answer: 4.0 infix: 5 +7 postfix: 57+ answer: 12.0 infix: 7*5 postfix: 7 5 * answer: 35.0 infix: (5-3) postfix: 5 3- answer: 2.0 infix: 5/5 postfix: 5 5/ answer: 1.0 infix: 8*5+3 postfix: 8 5 * 3 + answer: 43.0 infix: 8(5+3) postfix: 85 3+* answer: 64.0 infix: 8+3*5-7 postfix: 8 3 5* +7 - answer: 16.0 infix: (8+3)+(5-6) postfix: 83+56 + answer: -11.0 infix: ((8+3)+(2-7)) postfix: 83+27+ answer: -55.0 infix: ((8+3)+2)-7 postfix: 8 3 + 2 * 7 - answer: 15.0 infix: (8+5)+((3-2)-7*3) postfix: 8 5 * 3 2 - 7 3* answer: 20.0 infix: ((8*5+3)-7)-(5*3) postfix: 8 5 * 3 + 753 * answer: 21.0 infix: 7*9+7-5*6+3-4 postfix: 7 9 * 7 + 5 6* 3 + 4 - answer: 39.0 Pseudocode Evaluate a Postfix Expression 1. Initialize a stack. 2. If next input is a number: Read the next input and push it onto the stack. 3. Else: Read the next character, which is an operator symbol. Use top and pop to get the two numbers off the top of the stack. Combine these two numbers with the operation. Push the result onto the stack. 4. Go to #2 while there is more of the expression to read. 5. There should be one element on the stack, which is the result. Return it. Infix to Postfix Pseudocode 1. Initialize stack to hold operation symbols and parenthesis. 2. If the next input is a left parenthesis: Read the left parenthesis and push it onto the stack. 3. else if the next input is a number or operand: Read the operand (or number) and write it to the output. 4. else if the next input is an operator: while (stack is not empty AND stack's top is not left parenthesis AND stack's top is an operation with equal or higher precedence than the next input symbol): Print the stack's top. Pop the stack's top. Print the stack's top. " Pop the stack's top. 5. else: Push the next operation symbol onto the stack Read and discard the next input symbol (should be a right parenthesis). Print the top operation and pop it. while stack's top is not a left parenthesis: Print next symbol on stack and pop stack. Pop and discard the last left parenthesis. 6. Go to #2 while there is more of the expression to read. 7. Print and pop any remaining operations on the stack. There should be no remaining left parentheses. 486876.840988.qx3zqy7 LAB ACTIVITY 4.29.1: Project 5: Stacks 0/100 LAB ACTIVITY 4.29.1: Project 5: Stacks Downloadable files data.txt Download 1 from stack import Stack 2 3 def eval postfix(expr): 4 5 pass 6 def in2post (expr): 7 8 pass 9 def main(): 10 2256 11 12 if return 0 name main 13 main() Current file: main.py 0/100 Load default template... LAB ACTIVITY 4.29.1: Project 5: Stacks Downloadable files data.txt Download 2 3 4 5 1 class Stack: def _init_(self): pass def push(self, item): 6 pass 7 8 def pop(self): 9 pass 10 11 12 13 14 15 16 17 18 def top(self): pass def size(self): pass def clear(self): pass 0/100 Current file: stack.py Load default template... 5 +7 7*5 (5-3) 5/5 8*5+3 8* (5+3) 8+3*5-7 (8+3)*(5-6) ((8+3)*(2-7)) ((8+3)*2)-7 (8*5)+((3-2)-7*3) ((8*5+3)-7)-(5*3) 7*9+7-5*6+3-4