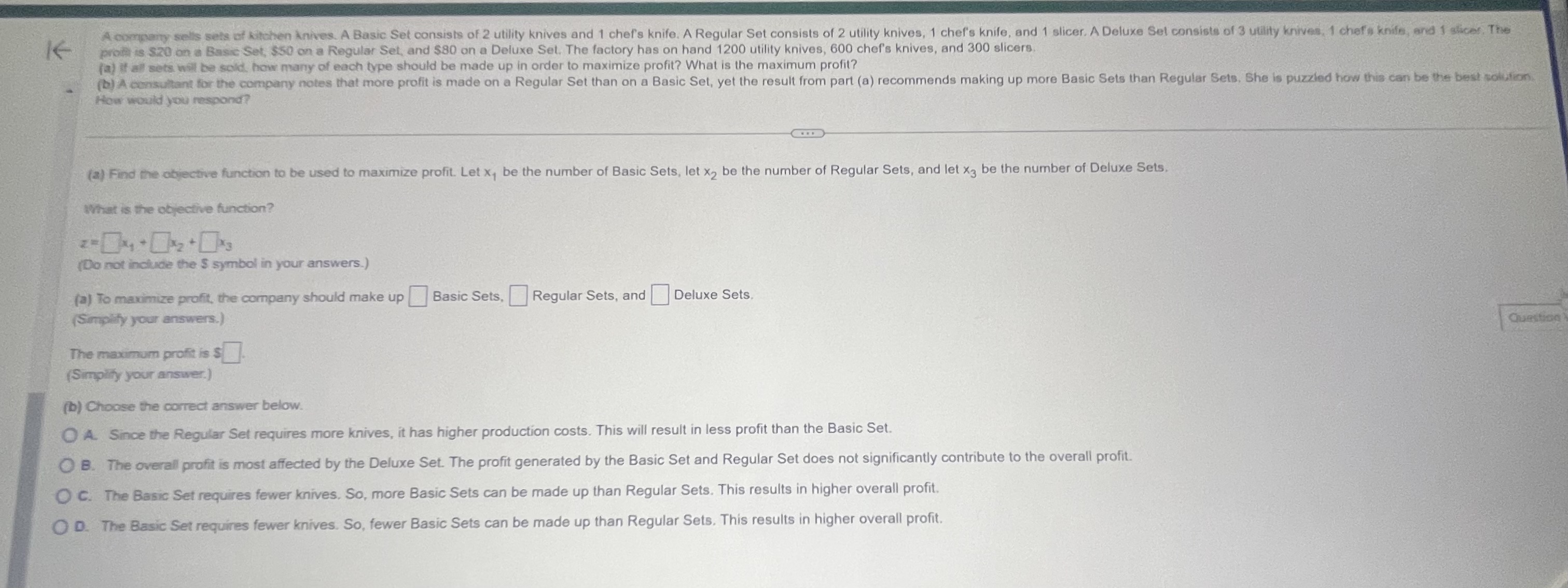
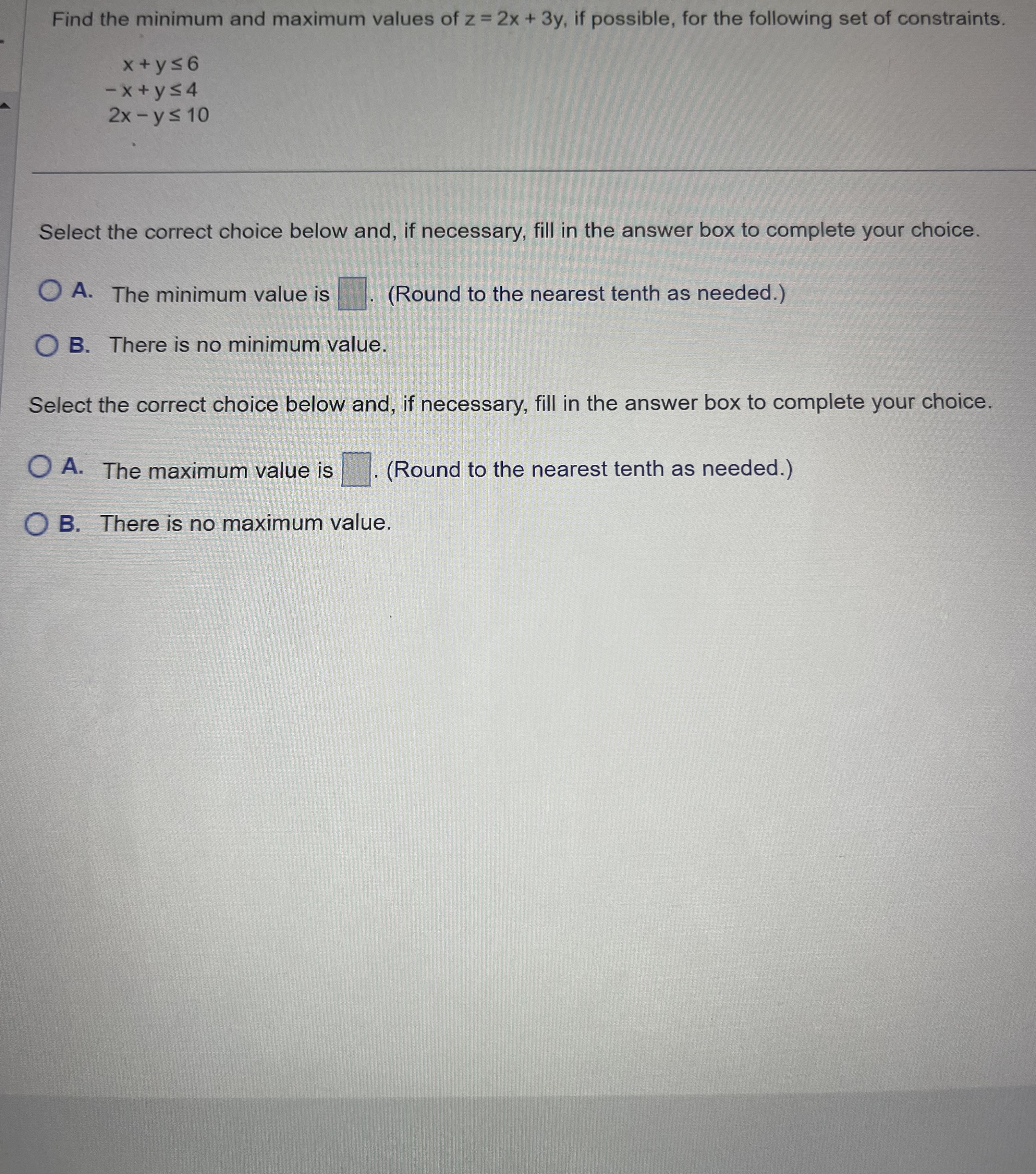
A company sells sets of kitchen knives. A Basic Set consists of 2 utility knives and 1 chef's knife. A Regular Set consists of 2 utility knives, 1 chef's knife, and 1 slicer, A Deluxe Set consists of 3 utility knives, 1 chef's knife, and 1 slices, The profil is $20 on a Basic Set, $50 on a Regular Set, and $80 on a Deluxe Set. The factory has on hand 1200 utility knives, 600 chef's knives, and 300 slicers. (a) if all sets will be sold, how many of each type should be made up in order to maximize profit? What is the maximum profit? (b) A consultant for the company notes that more profit is made on a Regular Set than on a Basic Set, yet the result from part (a) recommends making up more Basic Sets than Regular Sets, She is puzzled how this can be the best solution How would you respond? CD (a) Find the objective function to be used to maximize profit. Let x, be the number of Basic Sets, let X2 be the number of Regular Sets, and let x3 be the number of Deluxe Sets. What is the objective function? (Do not include the $ symbol in your answers.) (a) To maximize profit. the company should make up Basic Sets. Regular Sets, and Deluxe Sets. (Simplify your answers.) Question The maximum profit is s (Simplify your answer.) (b) Choose the correct answer below. A. Since the Regular Set requires more knives, it has higher production costs. This will result in less profit than the Basic Set. B. The overall profit is most affected by the Deluxe Set. The profit generated by the Basic Set and Regular Set does not significantly contribute to the overall profit. C. The Basic Set requires fewer knives. So, more Basic Sets can be made up than Regular Sets. This results in higher overall profit. O D. The Basic Set requires fewer knives. So, fewer Basic Sets can be made up than Regular Sets. This results in higher overall profit.A company is considering two insurance plans with coverage and premiums shown in the table. (For example, this means that $50 buys one unit Policy A Policy B of plan A. consisting of $10,000 fire and theft insurance and $180,000 of liability insurance.) Answer parts a and b. Fire/Theft $10,000 315,000 Liability $180,000 $120,000 Premium $50 $40 a. The company needs at least $450,000 fire and theft insurance and at least $4,800,000 liability from these plans. How many units should be purchased from each plan to minimize the cost of the premiums? What is the minimum premium? The company should purchase units of Policy A and units of Policy B. for a premium of $ b. Suppose the premium for policy A is reduced to $25. Now how many units should be purchased from each plan to minimize the cost of the premiums? What is the minimum premium? The company should purchase units of Policy A and units of Policy B, for a premium of $Find the minimum and maximum values of z = 2x + 3y, if possible, for the following set of constraints. xtys6 -x+ys4 2x - ys 10 Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. The minimum value is . (Round to the nearest tenth as needed.) O B. There is no minimum value. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. The maximum value is .(Round to the nearest tenth as needed.) O B. There is no maximum value