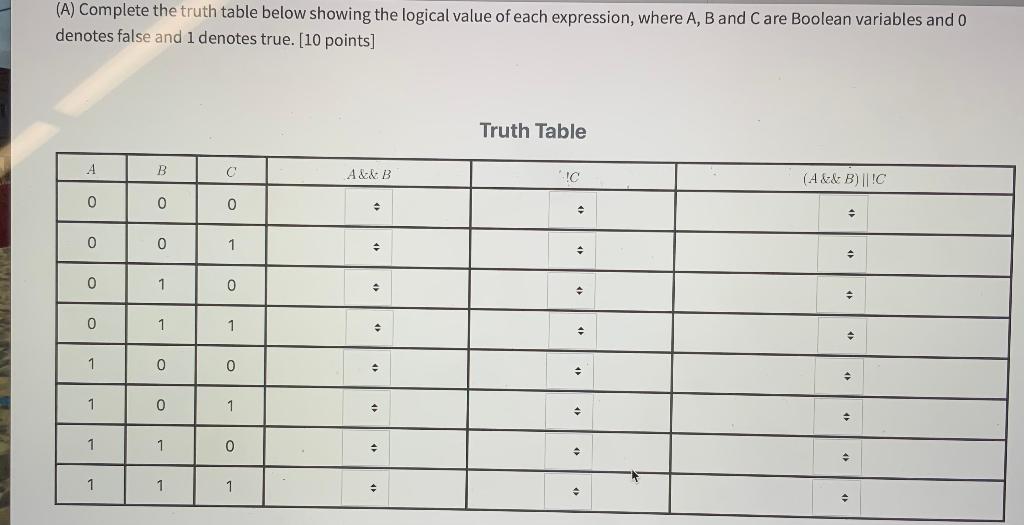
(A) Complete the truth table below showing the logical value of each expression, where A, B and Care Boolean variables and o denotes false and 1 denotes true. [10 points) Truth Table A B a A&&B !C (A&& B)||!C 0 0 o 0 0 1 0 1 0 . 0 1 1 + 1 0 0 1 0 1 1 1 0 + 1 1 1 (B) Suppose C represents the proposition "I have a car" and H represents the proposition "I have a house". Which of the C++ Boolean expressions below is logically equivalent to the statement "I do not have a house but I have a car"? [5 points] i.!C &&H II. C && !H iii.! CH iv. C || !H (C) Given the Boolean expression (single || !happy) && !poor, what set of values for the Boolean variables single, happy and poor that will make the expression true? [5 points) i. happy = true; poor=false; single=false ii. happy = true; poor=true; single=false iii. happy = false; poor=false; single=false iv. happy = false; poor=true; single=false V. NONE