a$)$ Consider an agent with utility function $u$:$\sqrt[\phantom{2}]{x}.$ He has a $($risky$)$ asset that gives $$100$ with probability $\frac{1}{2}$ and gives $$0$ with probability $\frac{1}{2}.$

Find the expected utility of the asset for the agent.

Consider also another agent who is identical to this one, in the sense that he has the same utility function and an asset that pays $$100$ with probability $\frac{1}{2}$ and gives $$0$ with probability $\frac{1}{2}.$ Assume throughout that what an asset pays is statistically independent from what the other asset pays. Imagine that the two agents form a mutual fund by pooling their assets, each agent owning half of the mutual fund.

$2.$ Compute each agent's share in the mutual fund.

$3.$ Calculate the agent's expected utility from the share in this mutual fund.

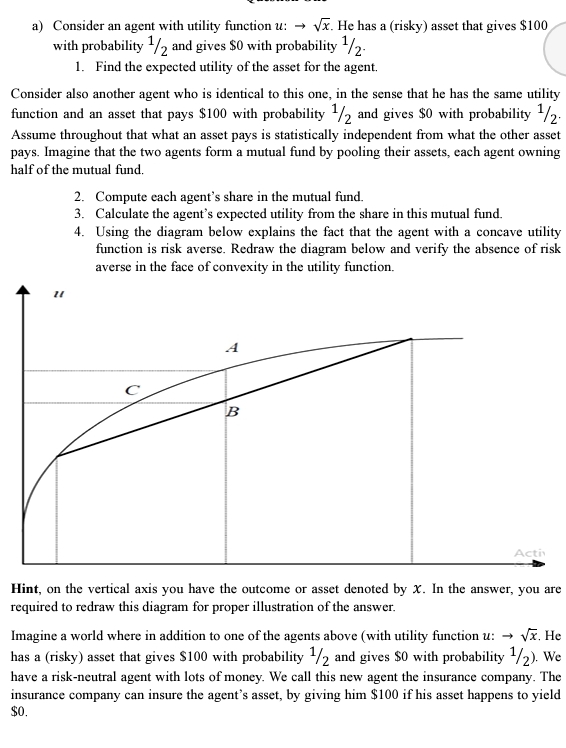
$4.$ Using the diagram below explains the fact that the agent with a concave utility function is risk averse. Redraw the diagram below and verify the absence of risk averse in the face of convexity in the utility function.

$11$

Hint, on the vertical axis you have the outcome or asset denoted by $x.$ In the answer, you are required to redraw this diagram for proper illustration of the answer.

Imagine a world where in addition to one of the agents above $($with utility function $u$:$\sqrt[\phantom{2}]{x}.$ He has a $($risky$)$ asset that gives $$100$ with probability $\frac{1}{2}$ and gives $$0$ with probability $\frac{1}{2}).$ We have a risk$-$neutral agent with lots of money. We call this new agent the insurance company. The insurance company can insure the agent's asset, by giving him $$100$ if his asset happens to yield $$0$