a) Consider the coordinate transformation given by x=(3u+v)/7,y=(4u?v)/7. Compute the absolute value of the Jacobian of x,y with respect to u,v b) Let ? be the second quadrant of the xy-plane, i.e. the region described by the inequalities x?0, y?0. Using the coordinate transform from part a evaluate

???e^(?t*(4x?3y)^2)dxdy

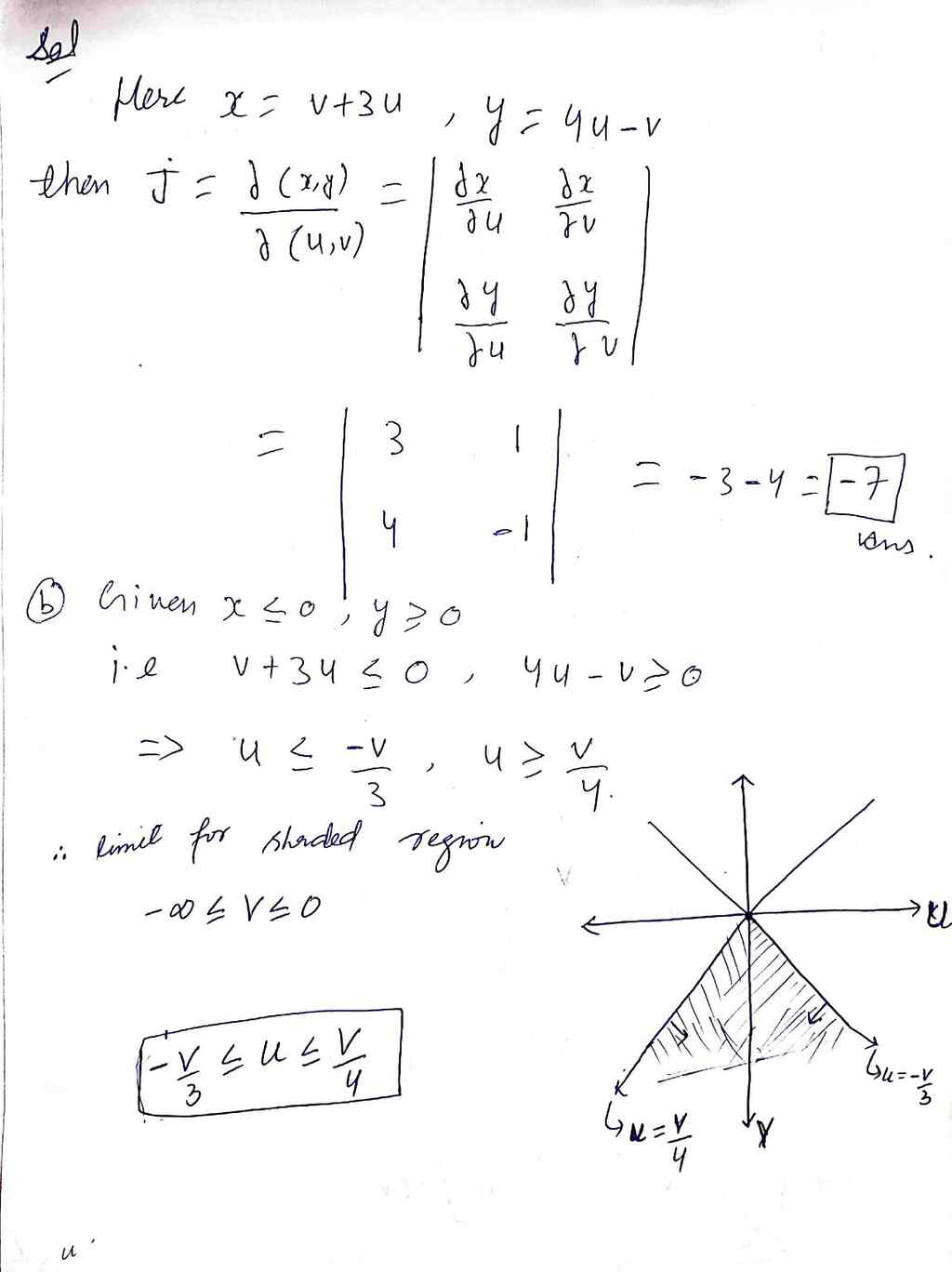
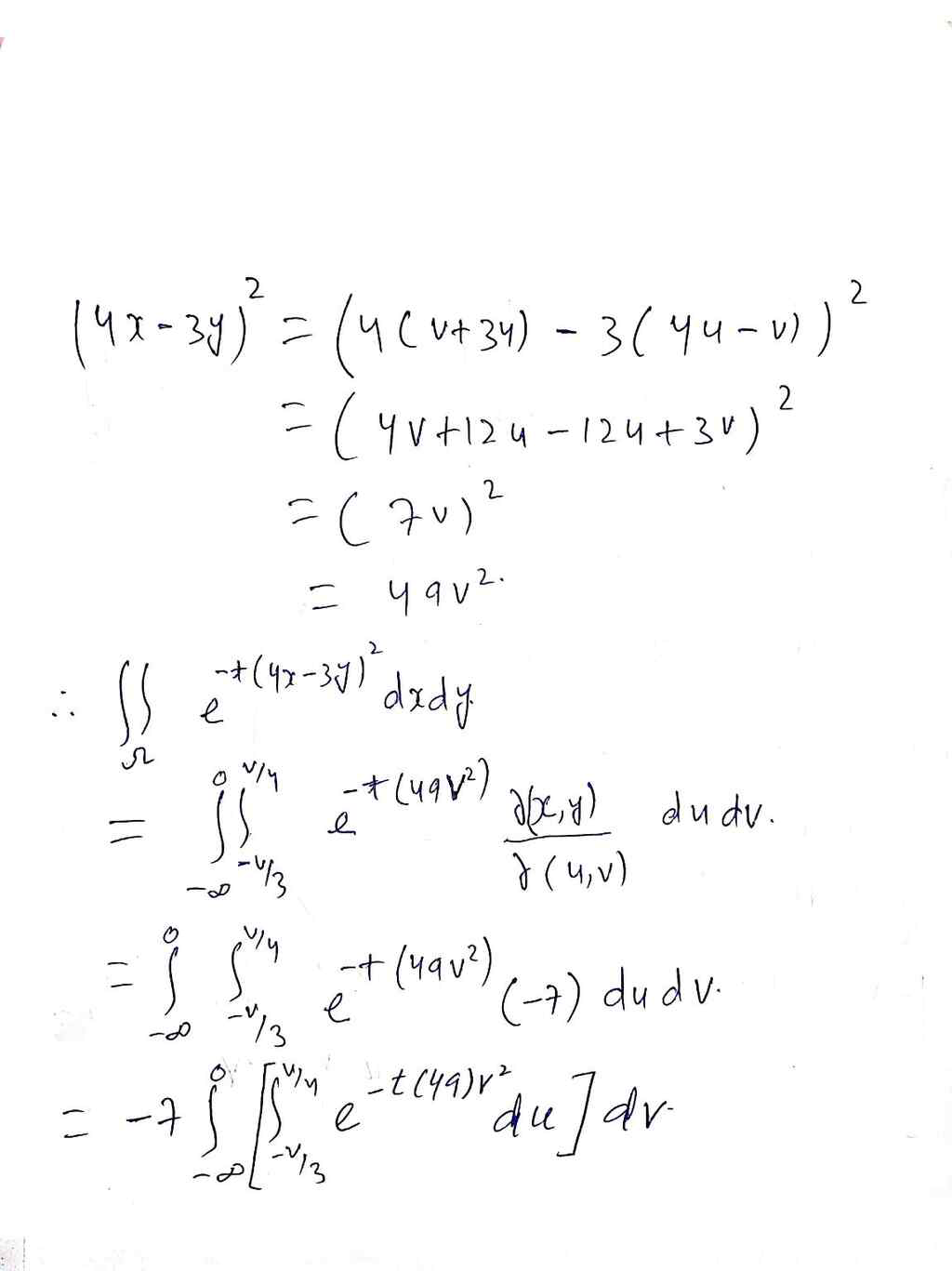
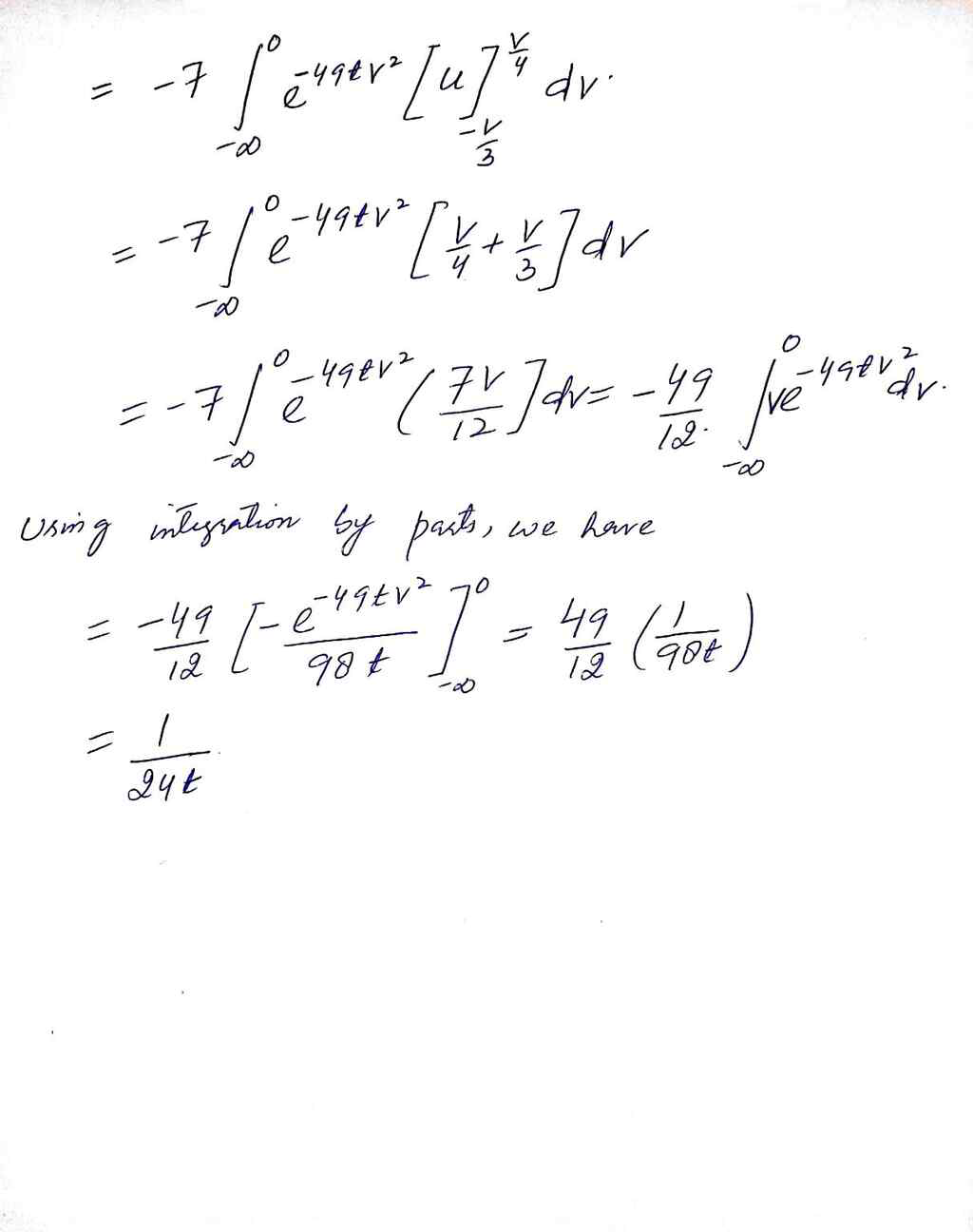
Sel More X = V + 3 0 , y = qu- V then J = I ( x,8 ) = dx a ( 4, V ) dy I V 3 - 2 - 3-4 - - 7 - 1 Given x so , y z V + 3 4 3 ". limit for shaded regrow - 0OL VSO - y bu= - u2 (4x- 34) = (4 (v+ 34) - 3 ( yu - V) ) = ( 4 v + 1 2 4 - 12 4 + 3 V ) 2 = ( 7 V ) 2 = 4 9 v2. 2 - * ( 4x - 37) dady . e O v/ y - * ( 49 vz ) abe, y ) dudv . - Of 7 ( 4, v ) vly -+ ( 4qv 2 ) e ( - 7 ) dudv. 13 v / y - t ( 4 9 ) v z e du / dv\f