Question: (a) Consider the influence function f(p) in Figure 7.13, which has four equi- libria p* = 0, and 1. Suppose we start with p(0)

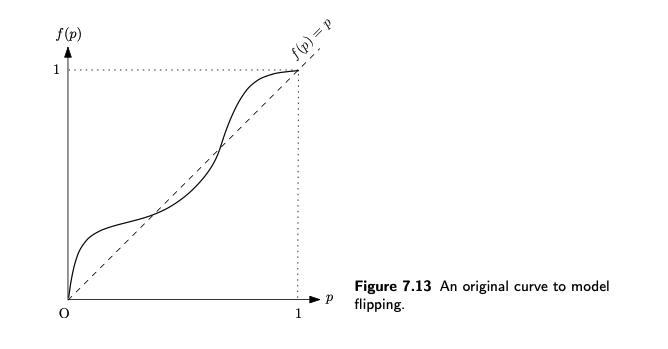
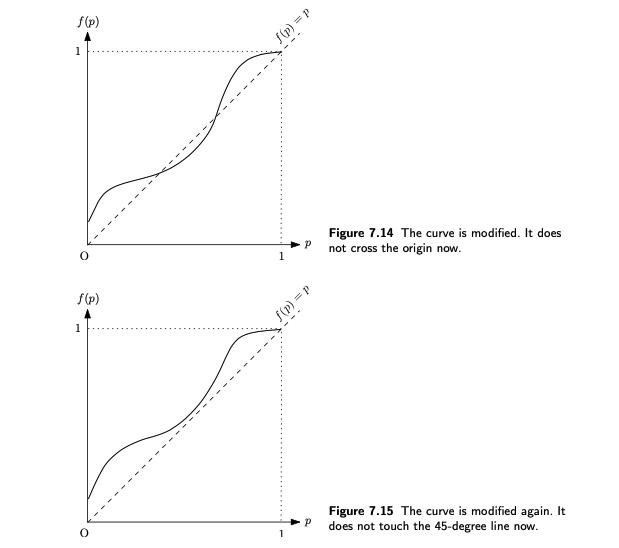
(a) Consider the influence function f(p) in Figure 7.13, which has four

equi- libria p* = 0, and 1. Suppose we start with p(0) = 0.01 (or some number slightly greater than 0). Find the equilibrium $fraction, denoted as Poo- f(p) 1 f(p) = p Figure 7.13 An$

(a) Consider the influence function f(p) in Figure 7.13, which has four equi- libria p* = 0, and 1. Suppose we start with p(0) = 0.01 (or some number slightly greater than 0). Find the equilibrium fraction, denoted as Poo- f(p) 1 f(p) = p Figure 7.13 An original curve to model flipping. f(p) 1 f(p) d = (d)f 1 P d = (d)f Figure 7.14 The curve is modified. It does not cross the origin now. P 1 Figure 7.15 The curve is modified again. It does not touch the 45-degree line now. (b) Suppose f(p) is slightly modified as in Figure 7.14, such that the point p=0 is no longer an equilibrium. Again use a graphical argument to find p(oo), starting at p(0) = 0. (c) Suppose f(p) is further slightly modified as in Figure 7.15, such that f(p)>p for 0 p < 1. Find p(oo) starting at p(0) = 0.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Programming Questions!

Let X be a random vector with multivariate Normal distribution N, (0,). Show that if rank() = p then X'-x~x(p). where x(p) denotes the chi-squared distribution with p degrees of freedom and X'...

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

can someone solve this Modern workstations typically have memory systems that incorporate two or three levels of caching. Explain why they are designed like this. [4 marks] In order to investigate...

Math230, 2017-18: Workshop, Coursework & Quiz Questions Coursework and Quiz marks The maximum mark obtainable through the handwritten coursework is 15 for CW01CW09. Each week there are two or three...

Examine the pricing strategies in the gasoline market. Make sure to address the following topics: In the article, (Mixed) Strategy in Oligopoly Pricing: Evidence from Gasoline Price Cycles Before and...

Algorithms in Artificial Intelligence (or, the old name: Introduction to Algorithmic Decision Making) Part 1 Based on slides by David Sarne and Lirong Xia Course Tentative Schedule Introduction...

Probability and Statistics - Problem Set c Keith M. Chugg October 2, 2015 1 Preliminaries, Combinatorics, Set Probability 1.1. A number of bats are in a cave. 2 bats can see out of their left eye. 3...

I need to know how to do the sections under Master It! and Solution Ross, Westerfield, Jaffe, and Jordan's Spreadsheet Master Corporate Finance, 11th edition by Brad Jordan and Joe Smolira Version...

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

Math\t107-6381\t-\tQuiz\t#4\t-\tSchultz\t-\tDue\tFebruary\t21,\t2016\t-\tpage\t1\tof 3 Follow\tthese\tdirections\tcarefully. This\tquiz\tis\tdue\tby\t11:59\tEastern\ttime\ton\tFebruary\t21,\t2016. o...

Hudson Corporation is considering three options for managing its data processing operation: continuing with its own staff, hiring an outside vendor to do the managing (referred to as outsourcing), or...

What are the key elements of a firms credit terms? What is a key determinant of the credit terms offered by a firm?

Exploring data in order to make correlation is is descriptive diagnostic predictive or descriptive analytic

Cold water (cp = 4.18 kJ/kg ¢ °C) leading to a shower enters a well-insulated, thin-walled, double-pipe, counter-flow heat exchanger at 15°C at a rate of 0.25 kg/s and is heated to...

Castellitto Company sells automatic can openers under a 75-day warranty for defective merchandise. Based on past experience, Castellitto estimates that 3% of the units sold will become defective...

Helium gas is compressed from 14 psia and 70F to 120 psia at a rate of 5 ft3/s. Determine the power input to the compressor, assuming the compression process to be (a) Isentropic, (b) Polytropic with...

Comprehensive problem with ABC costing. Pet Transport Company makes two pet carriers, the Cat-allac and the Dog-eriffic. They are both made of plastic with metal doors, but the Cat-allac is smaller....

Why do public utility companies usually have capital structures that are different from those of retail firms?

Can we put that she will be making weekly payroll deductions inthe amount of $52.75 to the housing equalling $211.00 monthly

In this exercise, we will explore some logical relationships between families of tastes that satisfy different assumptions. A: Suppose we define a strong and a weak version of convexity as follows:...

General Equilibrium Effects of a Property Tax: In Chapter 19, we introduced the idea that the property tax is really composed of two taxes: a tax on land, and a tax on improvements of land which we...

Compensating Wage Differentials and Increased Worker Safety: Why would any worker choose to work in a profession (like coal mining) that is risky for the workers health and safety? The answer is that...

Your friend Sam has been asked to prepare appetizers for the university reception. She has an unlimited amount of ingredients and 6 hours in which to prepare them. Sam can make 300 mini-sandwiches or...

Suppose you have a comparative advantage at baking cookies, and the other volunteer has a comparative advantage at baking cupcakes. Make a proposal to the volunteer about how to split up the baking....

Eleanor and her little sister Joanna are responsible for two chores on their familys farm: gathering eggs and collecting milk. Eleanor can gather 9 dozen eggs or collect 3 gallons of milk per week....