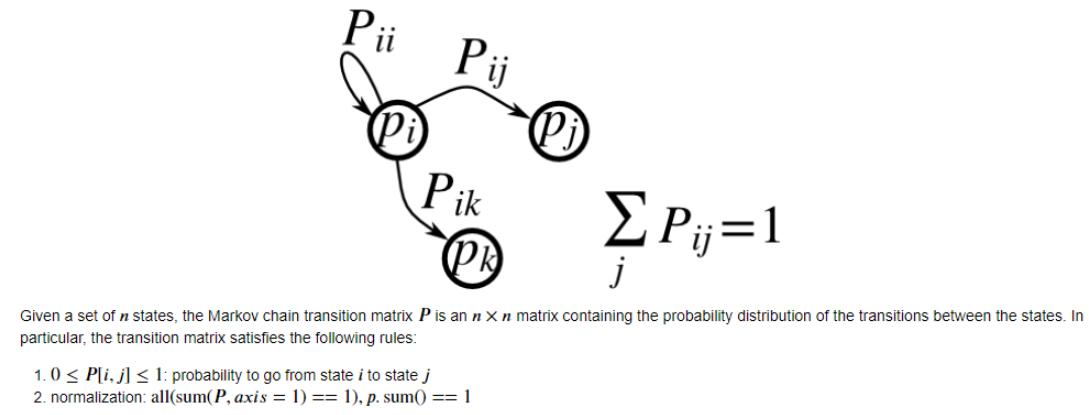
(a) Construct a 5 x 5 transition matrix P by starting from a random matrix and then normalize each row by dividing it by its row-sum, so that it is a transition Activate Windows matrix. Pii Pij Pik Pij=1 PR j Given a set of n states, the Markov chain transition matrix P is an n x n matrix containing the probability distribution of the transitions between the states. In particular, the transition matrix satisfies the following rules: (Pj 1.0 P[i, j] 1: probability to go from state i to state j 2. normalization: all(sum(P, axis = 1) == 1), p. sum() == 1