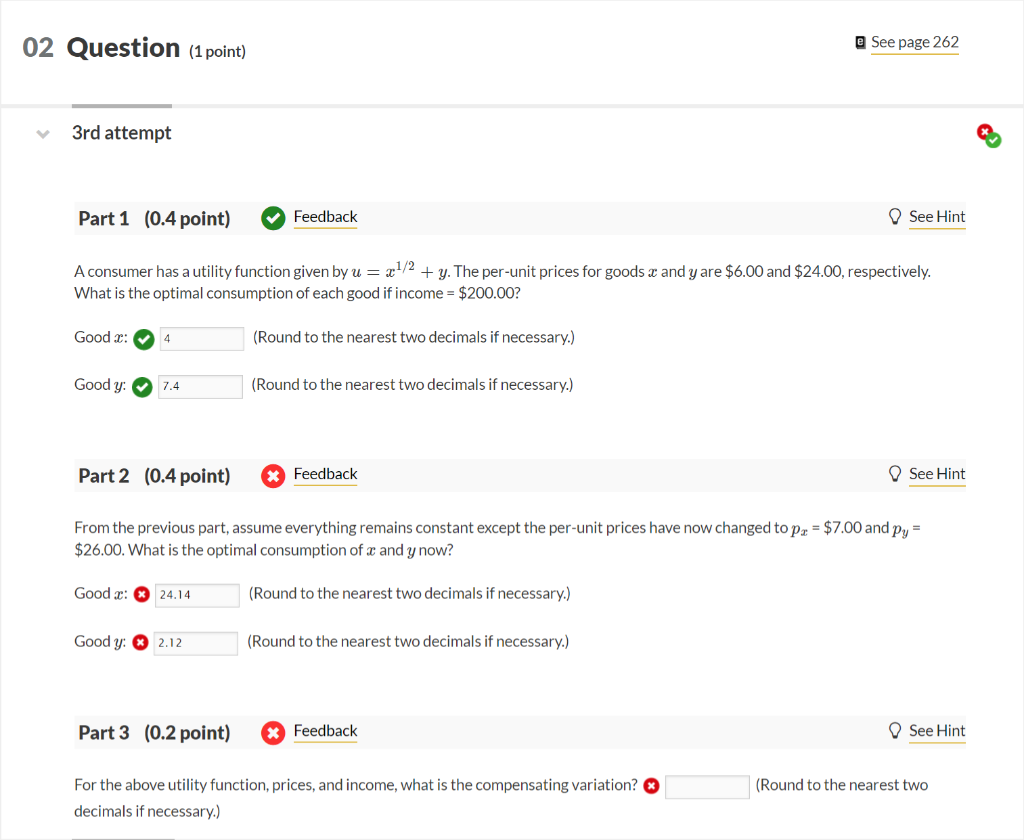
A consumer has a utility function given by u=x1/2+y. The per-unit prices for goods x and y are $6.00 and $24.00, respectively. What is the optimal consumption of each good if income =$200.00? Goodx (Round to the nearest two decimals if necessary.) Good y (Round to the nearest two decimals if necessary.) Part 2 ( 0.4 point) See His From the previous part, assume everything remains constant except the per-unit prices have now changed to px=$7.00 and py= $26.00. What is the optimal consumption of x and y now? Good x : (Round to the nearest two decimals if necessary.) Good y : (Round to the nearest two decimals if necessary.) Part 3 ( 0.2 point) For the above utility function, prices, and income, what is the compensating variation? (Round to the nearest two decimals if necessary.) A consumer has a utility function given by u=x1/2+y. The per-unit prices for goods x and y are $6.00 and $24.00, respectively. What is the optimal consumption of each good if income =$200.00? Goodx (Round to the nearest two decimals if necessary.) Good y (Round to the nearest two decimals if necessary.) Part 2 ( 0.4 point) See His From the previous part, assume everything remains constant except the per-unit prices have now changed to px=$7.00 and py= $26.00. What is the optimal consumption of x and y now? Good x : (Round to the nearest two decimals if necessary.) Good y : (Round to the nearest two decimals if necessary.) Part 3 ( 0.2 point) For the above utility function, prices, and income, what is the compensating variation? (Round to the nearest two decimals if necessary.)