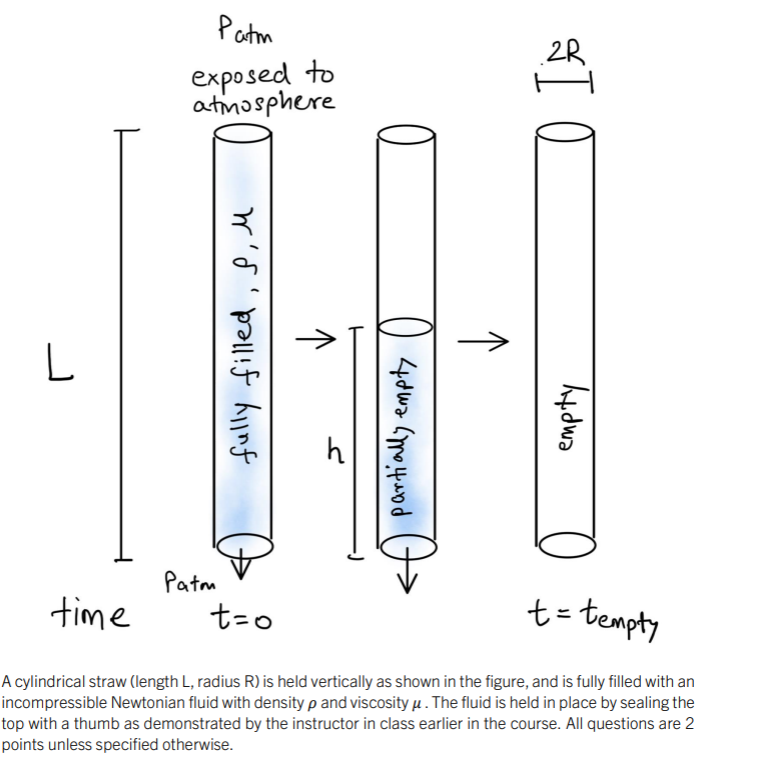
Question: A cylindrical straw ( length L , radius R ) is held vertically as shown in the figure, and is fully filled with an incompressible
A cylindrical straw length L radius R is held vertically as shown in the figure, and is fully filled with an incompressible Newtonian fluid with density rho and viscosity mu The fluid is held in place by sealing the top with a thumb as demonstrated by the instructor in class earlier in the course.
In practice a little cavity is created between the thumb and the top surface of the fluid. This overhead pressure ps is less than the atmospheric pressure patm The difference between the two pressures balances the gravitational forces on the fluid pointing downwards. Ignoring surface tension effects, calculate the overhead pressure ps for the full straw held static with a thumb blocking the top end. Use g as gravitational acceleration.
At t the thumb is removed, and the top end is now exposed to atmospheric pressure, creating a net draining force. Assuming you can ignore transient and surface tension effects and apply the HagenPoiseuille equation to obtain the expression for the instantaneous volumetric flow rate Q at the bottom.
At some time t after, the straw would be partially filled with a column of height h Assuming you can apply HagenPoiseuille equation at this precise moment, what is the instantaneous volumetric flow rate at the bottom as a function of height?
Interpret the equation derived from the previous part with respect to rho,muhR
Convert the previous equation in terms of height h of the column and its derivative with time, with no reference to Q in the final equation.
Integrate the previous equation from hL to h and t to ttempty to obtain an expression for tempty
Interpret the result for previous equation in terms of rho,muLR
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


