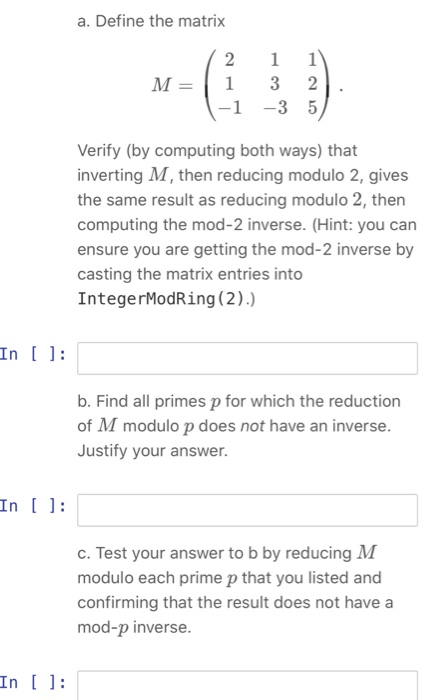
a. Define the matrix 2 M=| 1 1-1 1 3 -3 1 21. 5 Verify (by computing both ways) that inverting M, then reducing modulo 2, gives the same result as reducing modulo 2, then computing the mod-2 inverse. (Hint: you can ensure you are getting the mod-2 inverse by casting the matrix entries into IntegerModRing (2).) In [ ]: b. Find all primes p for which the reduction of M modulo p does not have an inverse. Justify your answer. In [ ]: c. Test your answer to b by reducing M modulo each prime p that you listed and confirming that the result does not have a mod-p inverse. In [ ]: a. Define the matrix 2 M=| 1 1-1 1 3 -3 1 21. 5 Verify (by computing both ways) that inverting M, then reducing modulo 2, gives the same result as reducing modulo 2, then computing the mod-2 inverse. (Hint: you can ensure you are getting the mod-2 inverse by casting the matrix entries into IntegerModRing (2).) In [ ]: b. Find all primes p for which the reduction of M modulo p does not have an inverse. Justify your answer. In [ ]: c. Test your answer to b by reducing M modulo each prime p that you listed and confirming that the result does not have a mod-p inverse. In [ ]