a. Design a non-recursive algorithm for computing an (discussed in the class). What is the basic operation? How many times is the algorithm's basic operation executed? b. Using an = a*an-1 (discussed in the class) to design a recursive algorithm for computing an . What is the basic operation? Set up and solve a recurrence relation for the number of times that algorithm's basic operation is executed. c. Using an = a*(a(n-1)/2) 2 (n is odd integer) and an = a*(an/2) 2 (n is even integer) (discussed in the class) to design a recursive algorithm for computing an . What is the basic operation? Set up and solve a recurrence relation for the number of times that algorithm's basic operation is executed.

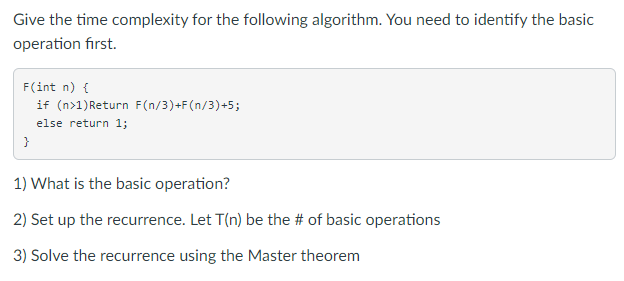
5. [12%] Give the time complexity for the following algorithm using two different approaches. You need to identify the basic operation first. F(int n) { If (n > 1) Return 2*F (n-1) ; Else Return 1; 1) [2%] What is the basic operation? 2) [2%]Set up the recurrence. Let T(n) be the # of basic operations. T(n) = 3) [4%] Use backward substitution to solve the recurrence and indicate the time complexity. 4) [4%] Write an iterative algorithm to solve the same problem.Give the time complexity for the following algorithm. You need to identify the basic operation first. F(int n) { if (n>1)Return F(n/3)+F(n/3)+5; else return 1; 1) What is the basic operation? 2) Set up the recurrence. Let T(n) be the # of basic operations 3) Solve the recurrence using the Master theorem