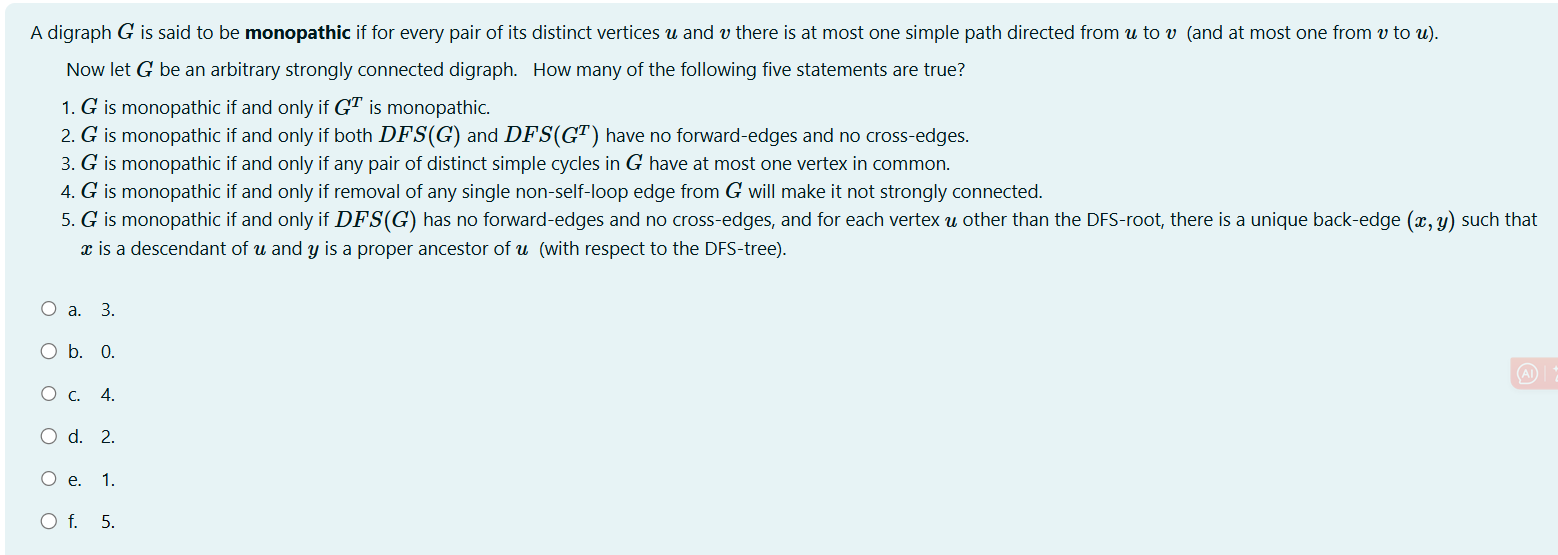
Question: A digraph ( G ) is said to be monopathic if for every pair of its distinct vertices ( u )
A digraph G is said to be monopathic if for every pair of its distinct vertices u and v there is at most one simple path directed from boldsymbolu to v and at most one from boldsymbolv to boldsymbolu
Now let G be an arbitrary strongly connected digraph. How many of the following five statements are true?
G is monopathic if and only if GT is monopathic.
G is monopathic if and only if both operatornameDFSG and operatornameDFSleftGTright have no forwardedges and no crossedges.
G is monopathic if and only if any pair of distinct simple cycles in G have at most one vertex in common.
G is monopathic if and only if removal of any single nonselfloop edge from G will make it not strongly connected.
G is monopathic if and only if D F SG has no forwardedges and no crossedges, and for each vertex u other than the DFSroot, there is a unique backedge x y such that boldsymbolx is a descendant of boldsymbolu and boldsymboly is a proper ancestor of boldsymboluwith respect to the DFStreeabCdef
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


