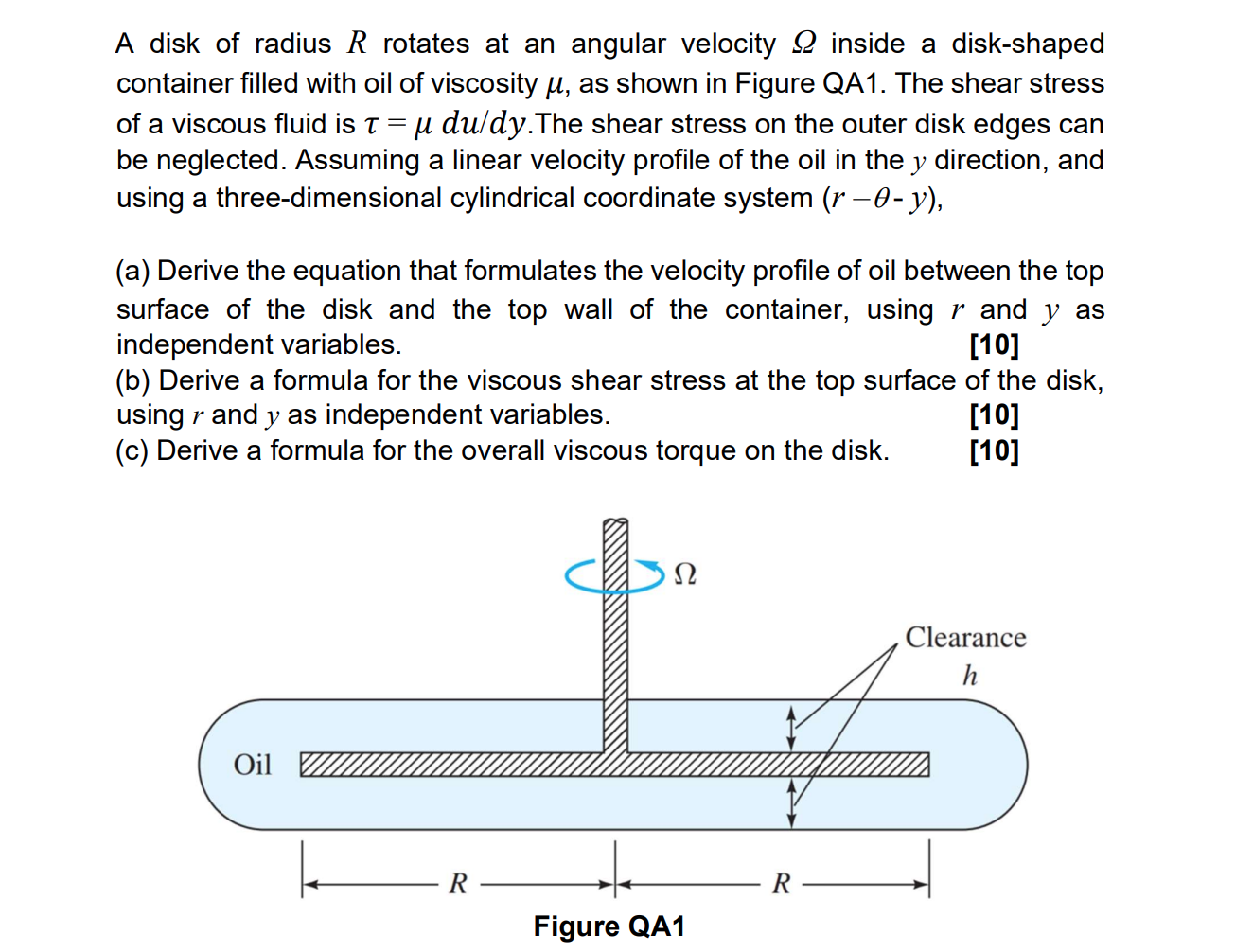
Question: A disk of radius ( R ) rotates at an angular velocity ( Omega ) inside a disk - shaped
A disk of radius R rotates at an angular velocity Omega inside a diskshaped container filled with oil of viscosity mu as shown in Figure QA The shear stress of a viscous fluid is taumu d u d y The shear stress on the outer disk edges can be neglected. Assuming a linear velocity profile of the oil in the y direction, and using a threedimensional cylindrical coordinate system rthetay
a Derive the equation that formulates the velocity profile of oil between the top surface of the disk and the top wall of the container, using r and y as independent variables.
b Derive a formula for the viscous shear stress at the top surface of the disk, using r and y as independent variables.
c Derive a formula for the overall viscous torque on the disk.
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


