$($a$)$ Does the population have to be normally distributed to test this hypothesis? Why?

A$.$ Yes, because $n30.$

B$.$ No$,$ because $n30.$

C$.$ No$,$ because the test is two$-$tailed.

D$.$ Yes, because the sample is random.

$($b$)$ If $\stackrel{}{x}=99\mathrm{.}9$ and $s=5\mathrm{.}9,$ compute the test statistic.

The test statistic is $t_0=,.($Round to two decimal places as needed.$)$

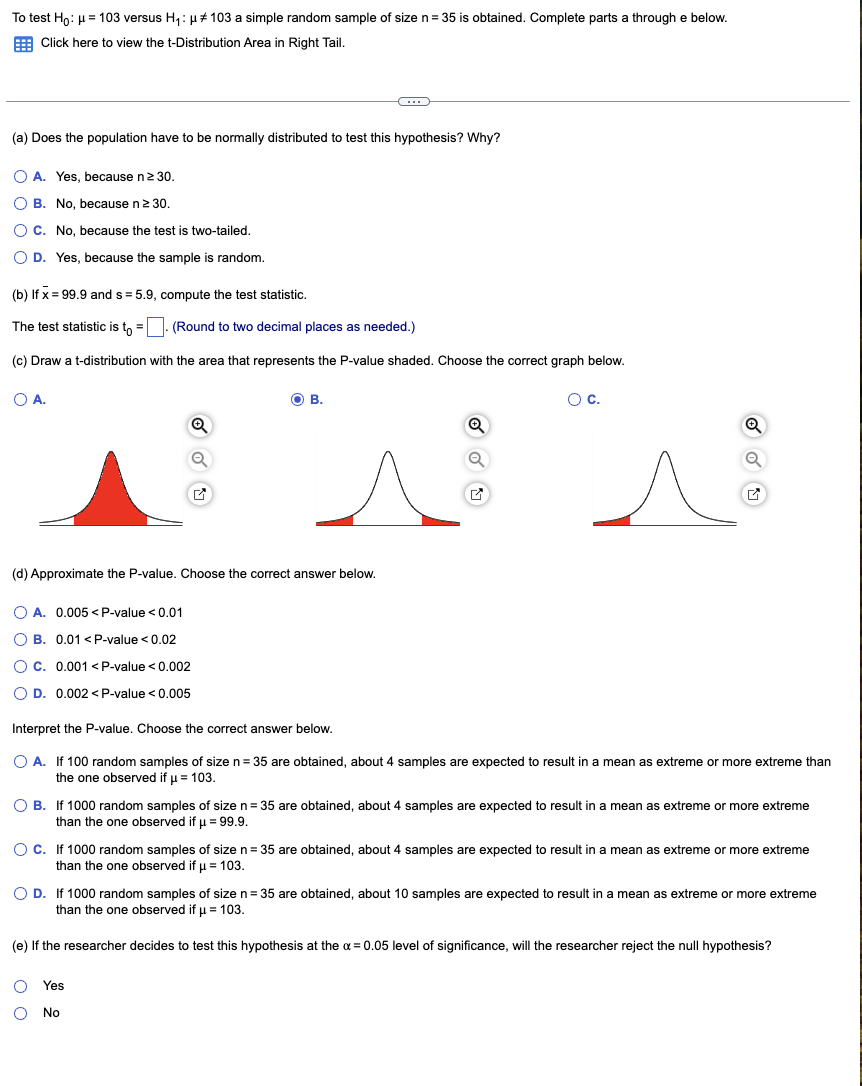
$($c$)$ Draw a t$-$distribution with the area that represents the P$-$value shaded. Choose the correct graph below.

$($d$)$ Approximate the P$-$value. Choose the correct answer below.

A$.0\mathrm{.}005$ P$-$value $<mn\; id="EditorElement\_22742">0</mn><mn\; id="EditorElement\_22743">.</mn><mn\; id="EditorElement\_22744">0</mn><mn\; id="EditorElement\_22745">1</mn>$

Bvalue $<mn\; id="EditorElement\_17683">0</mn><mn\; id="EditorElement\_17684">.</mn><mn\; id="EditorElement\_17685">0</mn><mn\; id="EditorElement\_17686">0</mn><mn\; id="EditorElement\_17687">2</mn>$

value $<mn\; id="EditorElement\_17722">0</mn><mn\; id="EditorElement\_17723">.</mn><mn\; id="EditorElement\_17724">0</mn><mn\; id="EditorElement\_17725">0</mn><mn\; id="EditorElement\_17726">5</mn>$

Interpret the $P-$value. Choose the correct answer below.

$A.If100$ random samples $of$ size $n=35$ are obtained, about $4$ samples are expected $to$ result $in$ a mean $as$ extreme $or$ more extreme than

the one observed $if=103.$

$B.If1000$ random samples $of$ size $n=35$ are obtained, about $4$ samples are expected $to$ result $in$ a mean $as$ extreme $or$ more extreme

than the one observed $if=99\mathrm{.}9.$

$C.If1000$ random samples $of$ size $n=35$ are obtained, about $4$ samples are expected $to$ result $in$ a mean $as$ extreme $or$ more extreme

than the one observed $if=103.$

$D.If1000$ random samples $of$ size $n=35$ are obtained, about $10$ samples are expected $to$ result $in$ a mean $as$ extreme $or$ more extreme

than the one observed $if=103.$

$(e)If$ the researcher decides $to$ test this hypothesis $at$ the $=0\mathrm{.}05$ level $of$ significance, will the researcher reject the null hypothesis?

Yes

$No0\mathrm{.}01-$value $<mn\; id="EditorElement\_19267">0</mn><mn\; id="EditorElement\_19268">.</mn><mn\; id="EditorElement\_19269">0</mn><mn\; id="EditorElement\_19270">2</mn>$

$C.0\mathrm{.}001-$value $<mn\; id="EditorElement\_19300">0</mn><mn\; id="EditorElement\_19301">.</mn><mn\; id="EditorElement\_19302">0</mn><mn\; id="EditorElement\_19303">0</mn><mn\; id="EditorElement\_19304">2</mn>$

value $<mn\; id="EditorElement\_19339">0</mn><mn\; id="EditorElement\_19340">.</mn><mn\; id="EditorElement\_19341">0</mn><mn\; id="EditorElement\_19342">0</mn><mn\; id="EditorElement\_19343">5</mn>$

Interpret the $P-$value. Choose the correct answer below.

$A.If100$ random samples $of$ size $n=35$ are obtained, about $4$ samples are expected $to$ result $in$ a mean $as$ extreme $or$ more extreme than

the one observed $if=103.$

$B.If1000$ random samples $of$ size $n=35$ are obtained, about $4$ samples are expected $to$ result $in$ a mean $as$ extreme $or$ more extreme

than the one observed $if=99\mathrm{.}9.$

$C.If1000$ random samples $of$ size $n=35$ are obtained, about $4$ samples are expected $to$ result $in$ a mean $as$ extreme $or$ more extreme

than the one observed $if=103.$

$D.If1000$ random samples $of$ size $n=35$ are obtained, about $10$ samples are expected $to$ result $in$ a mean $as$ extreme $or$ more extreme

than the one observed $if=103.$

$(e)If$ the researcher decides $to$ test this hypothesis $at$ the $=0\mathrm{.}05$ level $of$ significance, will the researcher reject the null hypothesis?

Yes

$No$