Question: A firm has prepared the following binary integer program to evaluate a number of potential locations for new warehouses. The firm's goal is to maximize

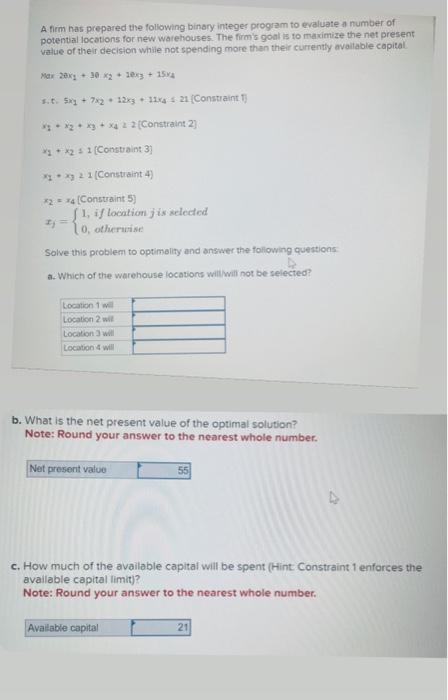
A firm has prepared the following binary integer program to evaluate a number of potential locations for new warehouses. The firm's goal is to maximize the net present value of their decision while not spending more than their currently avaliable capital. Max20x1+36x2+10x3+15y41.5.5x1+7x2+12x3+11x421(Constraint1)x3+x2+x3+x422[Constraint2]x1+x21[Contraint3]x1x31(Constraint4)x2=x4[Constraint5]xj={1,iflocationjisselected0,otherwise Solve this problem to optimality and answer the following questions: a. Which of the warehouse locations will will not be selected? b. What is the net present value of the optimal solution? Note: Round your answer to the nearest whole number. c. How much of the available capital will be spent (Hint: Constraint 1 enforces the available capital limity? Note: Round your answer to the nearest whole number

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Finance Questions!

please answer A,B,C right A firm has prepared the following binary integer program to evaluate a number of potential locations for new warehouses. The firm's goal is to maximize the net present value...

A firm has prepared the following binary integer program to evaluate a number of potential locations for new warehouses. The firms goal is to maximize the net present value of their decision while...

A firm has prepared the following binary integer program to evaluate a number of potential locations for new warehouses. The firm s goal is to maximize the net present value of their decision while...

solve soon A firm has prepared the following binary integer program to evaluate a number of potential locations for new warehouses. The firm's goal is to maximize the net present value of their...

Need step-by-step solution via Excel Solver. From Chapter 7 of Introduction to Manage Science: A Modeling and Case Studies Approach with Spreadsheets (Fredrick Hillier, 6th Edition.) Please open...

A firm has prepared the following binary Integer program to evaluate a number of potential locations for new warehouses. The firm's goal is to maximize the net present value of their decision while...

What multiple of the time constant gives the time taken by an initially uncharged capacitor in an RC series circuit to be charged to 99.0% of its final charge?

Based on the forecasts from Exercise 3, construct a 95% interval forecast for the returns of each of the three series. Assume that the 1-step-ahead forecast of the return is zero and that the returns...

Muse Company commences business on 1 January Year 2 0 0 9 , adjusted its provision for doubtful debts at the end of each year by 5 % of its net debtors. Below are the details for the year ended for 3...

On 1 March 2007 DB Limited issued R560 000 15% debentures at R98. The debentures were to be redeemed at par in four equal annual payments starting 28 February 2010. Required: Journalise the above...