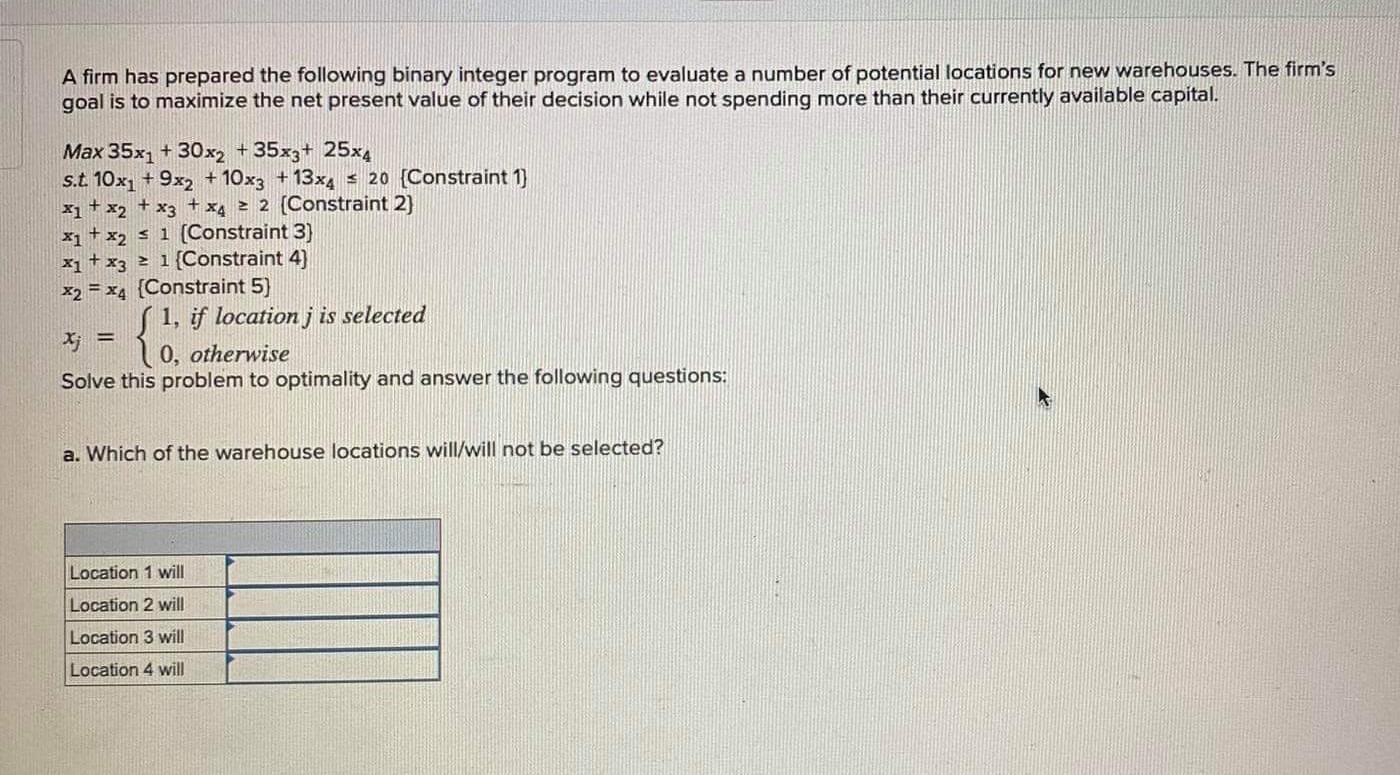
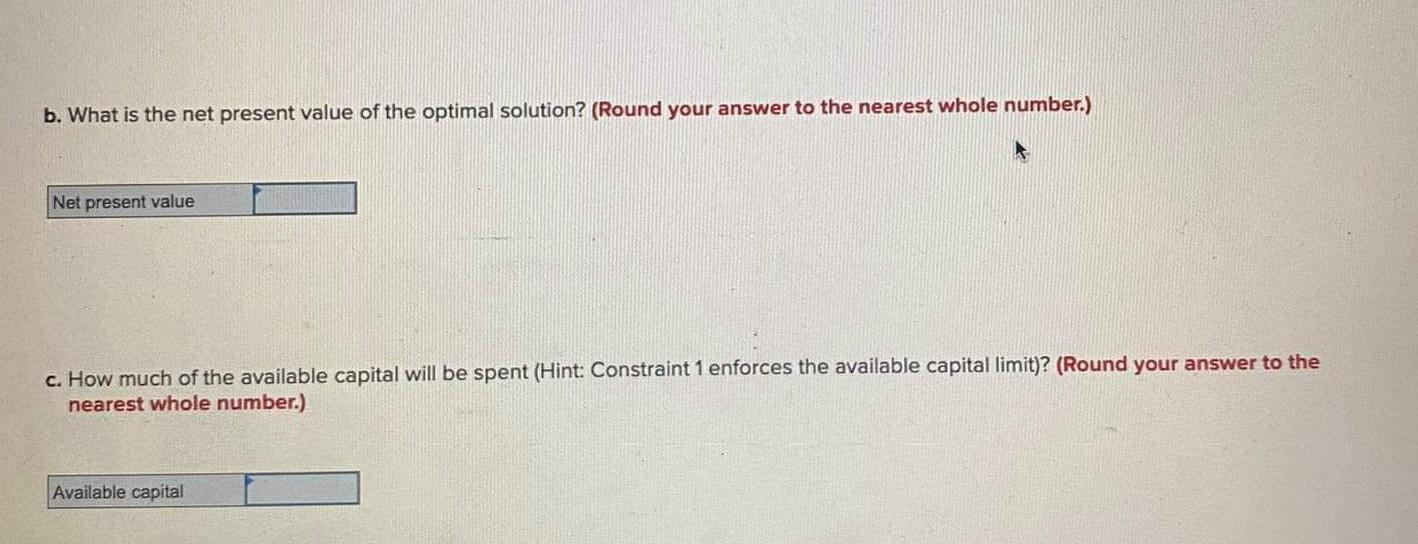
A firm has prepared the following binary integer program to evaluate a number of potential locations for new warehouses. The firm's goal is to maximize the net present value of their decision while not spending more than their currently available capital. + Max 35x + 30x2 + 35x3+ 25x4 s.t 10x + 9x2 + 10x3 + 13x4 20 [Constraint 1) x1 + x2 + x3 + x4 2 2 (Constraint 2] x1 + x2 1 (Constraint 3) x1 + x3 = 1 (Constraint 4) x2 = x4 Constraint 5) 1, if location j is selected X;= 0, otherwise Solve this problem to optimality and answer the following questions: a. Which of the warehouse locations will/will not be selected? Location 1 will Location 2 will Location 3 will Location 4 will b. What is the net present value of the optimal solution? (Round your answer to the nearest whole number.) Net present value c. How much of the available capital will be spent (Hint: Constraint 1 enforces the available capital limit)? (Round your answer to the nearest whole number.) Available capital