A flexible cable suspended between two vertical supports is hanging under its own weight. The weight of a horizontal roadbed is distributed evenly along the x-axis with the density =0.3=0.3 lb/ft. The coordinate system is chosen so that the y-axis passes through the lowest point 1P1 and the x-axis is =2a=2 ft below 1P1. If the absolute value of tension force in the cable at point 1P1 is =1T=1, then the initial value problem that governs the shape of the cable is (Use the notation /dy/dx for the first derivative)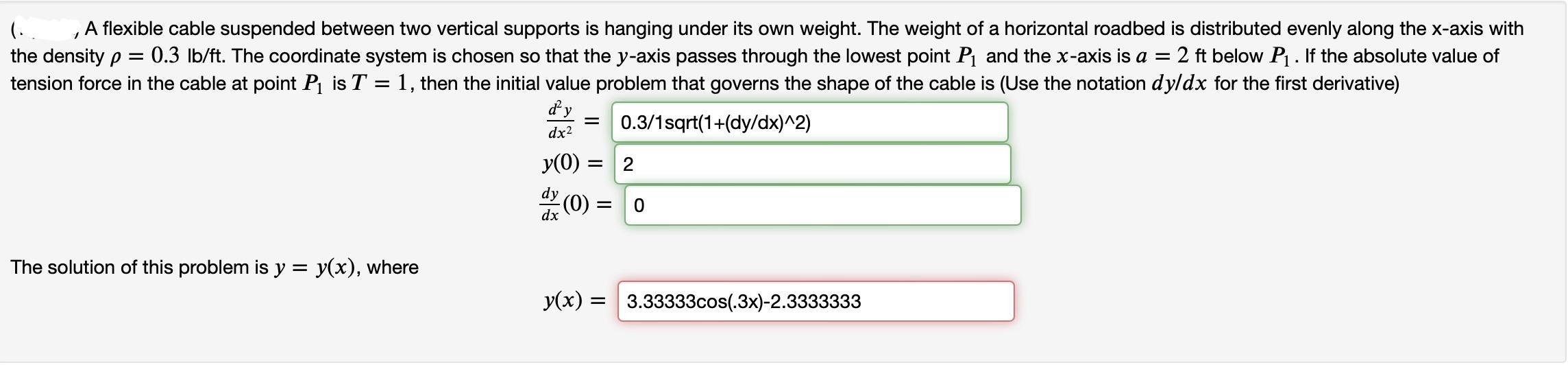

(. , A flexible cable suspended between two vertical supports is hanging under its own weight. The weight of a horizontal roadbed is distributed evenly along the x-axis with the density =0.3lb/ft. The coordinate system is chosen so that the y-axis passes through the lowest point P1 and the x-axis is a=2 ft below P1. If the absolute value of tension force in the cable at point P1 is T=1, then the initial value problem that governs the shape of the cable is (Use the notation dy/dx for the first derivative) dx2d2y=y(0)=dxdy(0)= The solution of this problem is y=y(x), where y(x)=