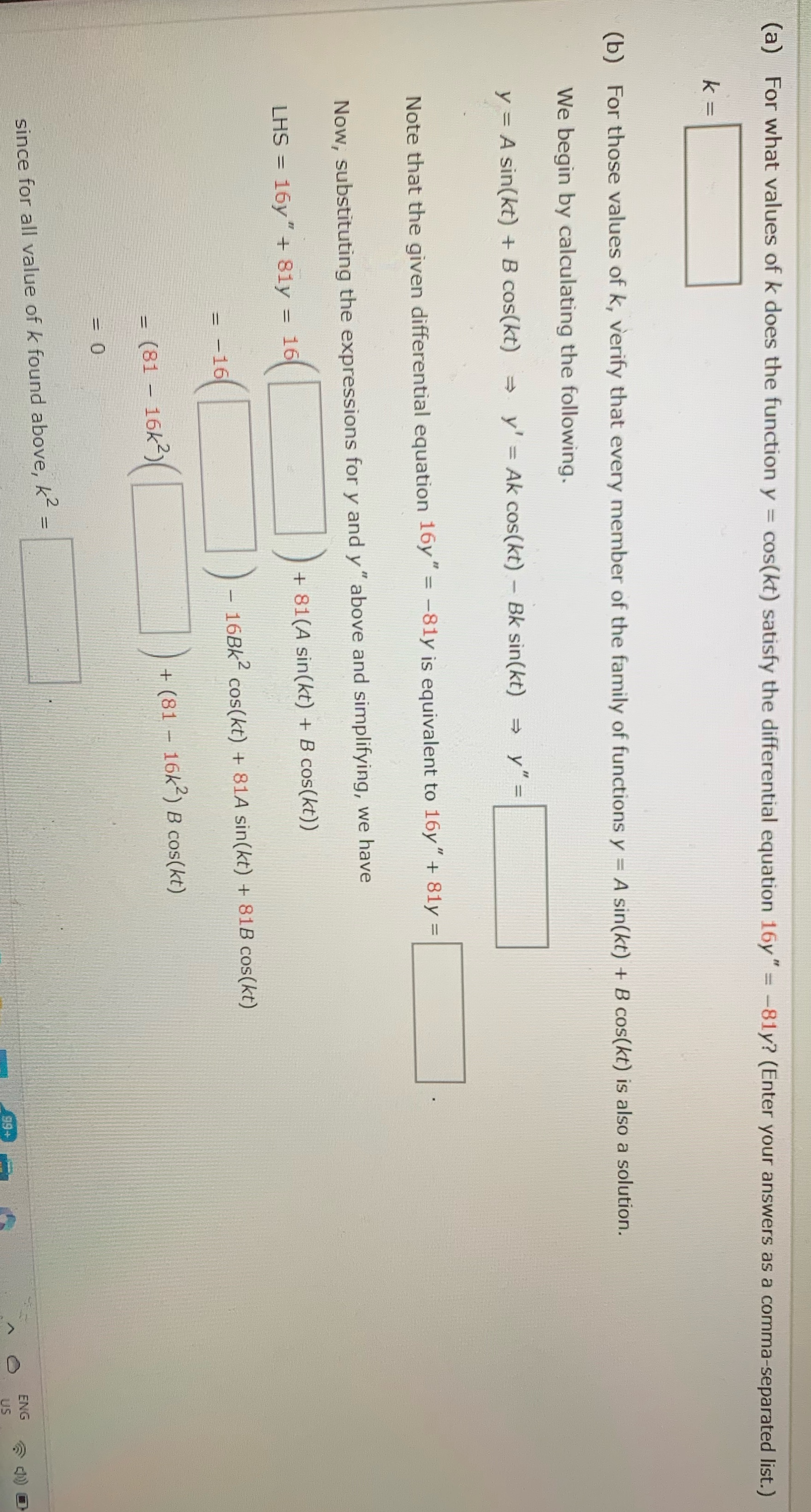
(a) For what values of k does the function y = cos(kt) satisfy the differential equation 16y" = -81y? (Enter your answers as a comma-separated list.) = (b) For those values of k, verify that every member of the family of functions y = A sin(kt) + B cos(kt) is also a solution. We begin by calculating the following. y = A sin(kt) + B cos(kt) = y' = Ak cos(kt) - Bk sin(kt) = y" = Note that the given differential equation 16y " = -81y is equivalent to 16y " + 81y = Now, substituting the expressions for y and y " above and simplifying, we have LHS = 16y " + 81y = 16 + 81(A sin(kt) + B cos(kt)) = -16 - 16BK cos(kt) + 81A sin(kt) + 81B cos(kt) = (81 - 16/2) + (81 - 16k2) B cos(kt) = 0 since for all value of k found above, k2 = 99+ O ENG