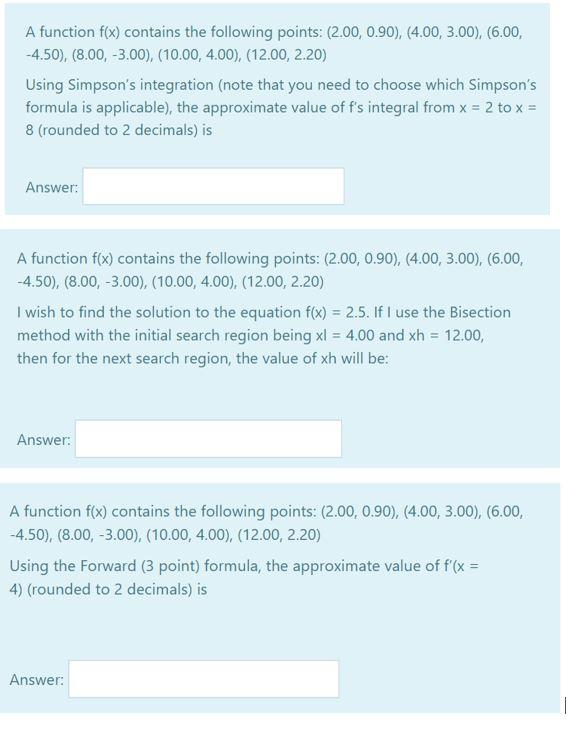
A function f(x) contains the following points: (2.00, 0.90), (4.00, 3.00), (6.00, -4.50), (8.00, -3.00), (10.00, 4.00), (12.00, 2.20) Using Simpson's integration (note that you need to choose which Simpson's formula is applicable), the approximate value of f's integral from x = 2 to x = 8 (rounded to 2 decimals) is Answer: A function f(x) contains the following points: (2.00, 0.90), (4.00, 3.00), (6.00, -4.50), (8.00, -3.00), (10.00, 4.00), (12.00, 2.20) I wish to find the solution to the equation f(x) = 2.5. If I use the Bisection method with the initial search region being xl = 4.00 and xh = 12.00, then for the next search region, the value of xh will be: Answer: A function f(x) contains the following points: (2.00, 0.90), (4.00, 3.00), (6.00, -4.50), (8.00, -3.00), (10.00, 4.00), (12.00, 2.20) Using the Forward (3 point) formula, the approximate value of f(x = 4) (rounded to 2 decimals) is