A Gaussian beam is transmitted through a thin lens of focal length f.

(a) Show that the locations of the waists of the incident and transmitted beams, z and z', respectively, are related by

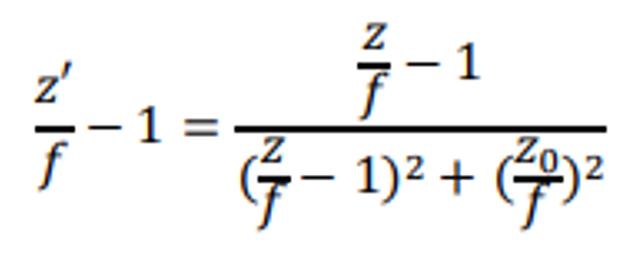
(b) The beam is collimated by making the location of the new waist z' as distant as possible from the lens. This is achieved by using the smallest possible ratio z ₀ /f(short depth of focus and long focal length). For a given ratio z ₀ /f, show that the optimal value of z for collimation is z = f + z ₀ . [Hint: The optimal value of z occurs when (z'/f-1) reaches its maximum value.]

(c) Given λ = 1 μm, z ₀ = 1 cm and f = 50 cm, determine the optimal value of z for collimation, and the corresponding magnification M, distance z', and width W ₀ ' of the collimated beam.

z' 1 1 1 : G- 1)2 + (4)2