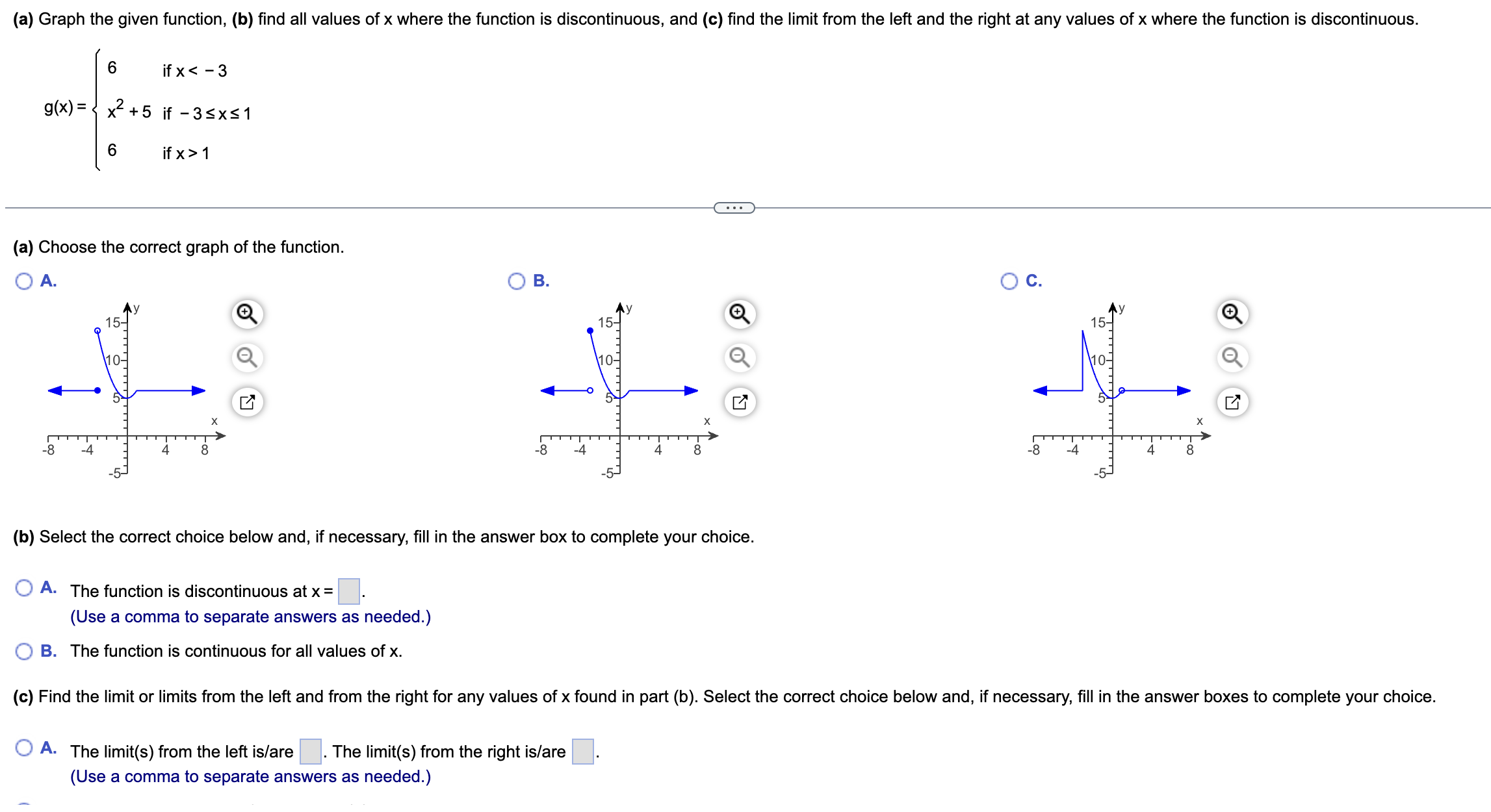
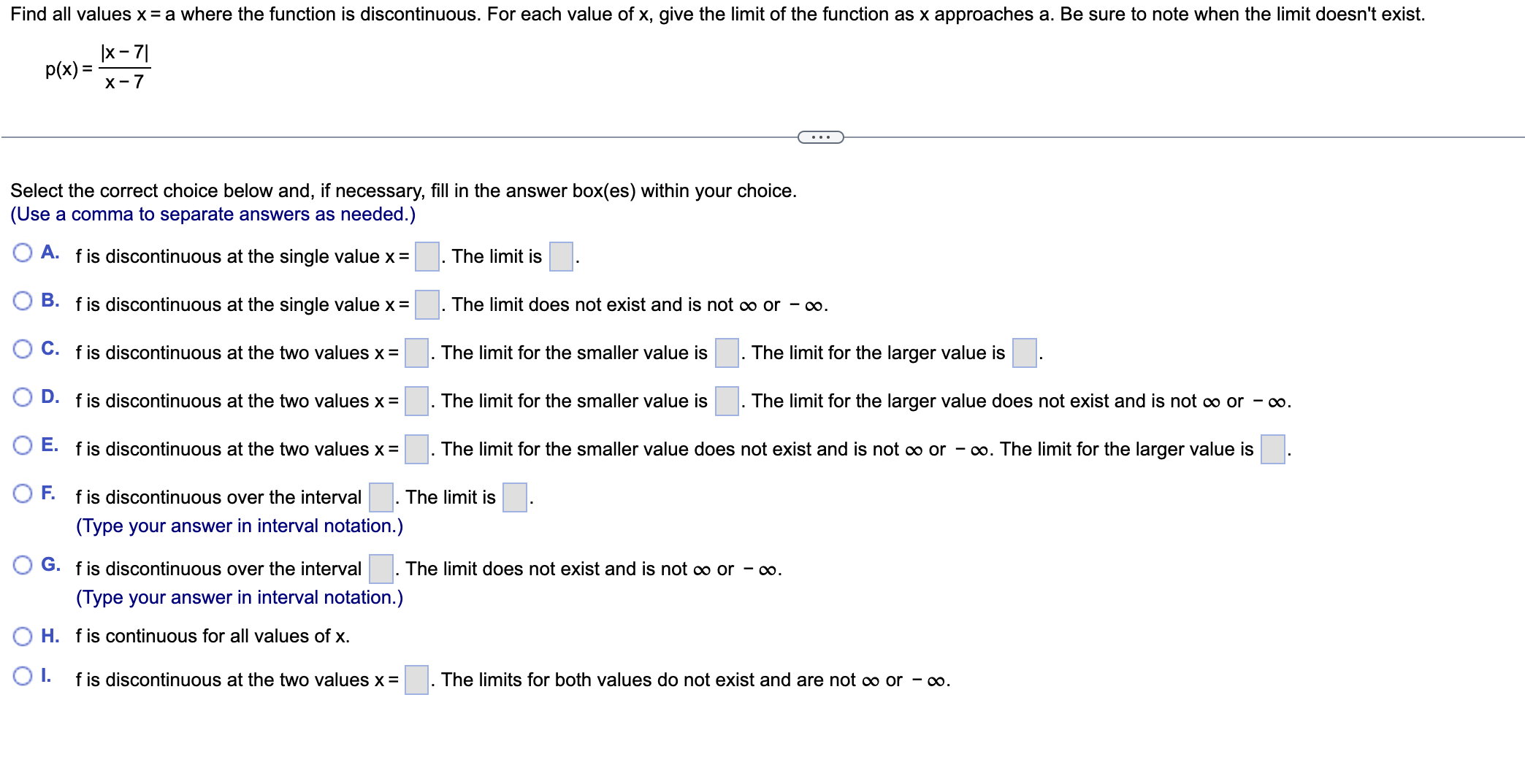
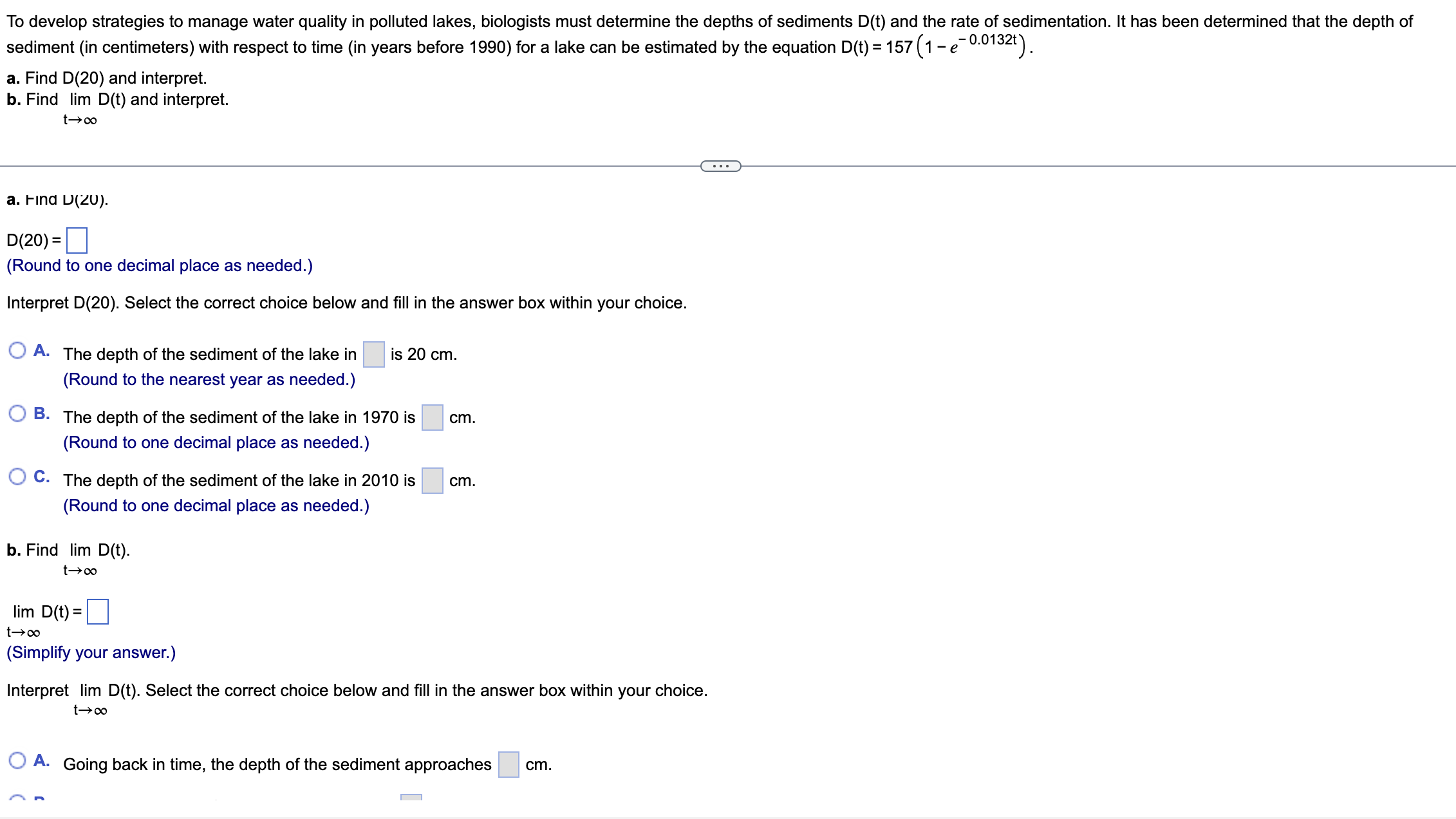
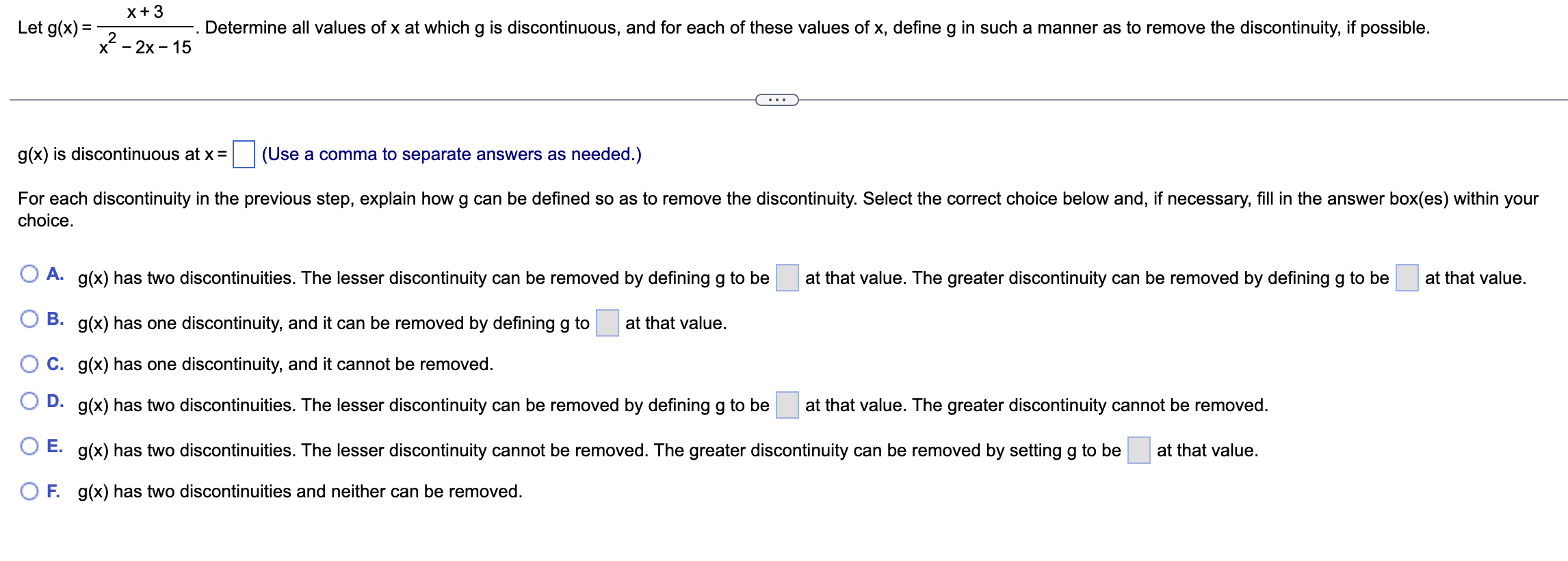
(a) Graph the given function, (b) find all values of x where the function is discontinuous, and (c) find the limit from the left and the right at any values of x where the function is discontinuous. 6 if x 1 (a) Choose the correct graph of the function. O A. O B. O c. 15- 15- 10- 10- 10- X X X 8 8 -4 8 (b) Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. The function is discontinuous at x = (Use a comma to separate answers as needed.) O B. The function is continuous for all values of x. (c) Find the limit or limits from the left and from the right for any values of x found in part (b). Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice. O A. The limit(s) from the left is/are . The limit(s) from the right is/are (Use a comma to separate answers as needed.)Find all values x = a where the function is discontinuous. For each value of x, give the limit of the function as x approaches a. Be sure to note when the limit doesn't exist. |X - 71 p(x) = x - 7 Select the correct choice below and, if necessary, fill in the answer box(es) within your choice. (Use a comma to separate answers as needed.) O A. f is discontinuous at the single value x = The limit is O B. f is discontinuous at the single value x = The limit does not exist and is not co or - co. O C. f is discontinuous at the two values x = The limit for the smaller value is The limit for the larger value is O D. f is discontinuous at the two values x = The limit for the smaller value is . The limit for the larger value does not exist and is not co or - co. O E. f is discontinuous at the two values x = . The limit for the smaller value does not exist and is not co or - co. The limit for the larger value is O F. f is discontinuous over the interval . The limit is (Type your answer in interval notation.) O G. f is discontinuous over the interval . The limit does not exist and is not co or - co. (Type your answer in interval notation.) O H. f is continuous for all values of x. O I. f is discontinuous at the two values x = The limits for both values do not exist and are not co or - co.Find the value x=a where the function is discontinuous. For the point of discontinuity, give (a) f(a) if it exists, (b) lim f(x), (c) lim f(x), (d) lim f(x), and (e) f(x) x>a x>a'r x)a identify which conditions for continuity are not met. a = (Use a comma to separate answers as needed.) (a) Select the choice below and, if necessary, ll in the answer box within your choice. (:3 A. f(a): [1:3 B. f(a) is undefined. (b) Select the choice below and, if necessary, ll in the answer box within your choice. {:3 A. lim f(x) = X)a {:3 B. lim f(x) does not exist. X>a (0) Select the choice below and, if necessary, ll in the answer box within your choice. CZ? A- lim f(x) = X>a+ To develop strategies to manage water quality in polluted lakes, biologists must determine the depths of sediments D(t) and the rate of sedimentation. It has been determined that the depth of sediment (in centimeters) with respect to time (in years before 1990) for a lake can be estimated by the equation D(t) = 157 (1 -e-0.0132t). a. Find D(20) and interpret. b. Find lim D(t) and interpret. a. Find D(20). D(20) = (Round to one decimal place as needed.) Interpret D(20). Select the correct choice below and fill in the answer box within your choice. O A. The depth of the sediment of the lake in is 20 cm. (Round to the nearest year as needed.) O B. The depth of the sediment of the lake in 1970 is cm. (Round to one decimal place as needed.) O C. The depth of the sediment of the lake in 2010 is cm. (Round to one decimal place as needed.) b. Find lim D(t). 1 -+ 00 lim D(t) = 1 -+ 0o (Simplify your answer.) Interpret lim D(t). Select the correct choice below and fill in the answer box within your choice. 1- 00 O A. Going back in time, the depth of the sediment approaches cx+ 3 Let g(x) = Determine all values of x at which g is discontinuous, and for each of these values of x, define g in such a manner as to remove the discontinuity, if possible. x2 - 2x - 15 g(x) is discontinuous at x = (Use a comma to separate answers as needed.) For each discontinuity in the previous step, explain how g can be defined so as to remove the discontinuity. Select the correct choice below and, if necessary, fill in the answer box(es) within your choice. A. g(x) has two discontinuities. The lesser discontinuity can be removed by defining g to be at that value. The greater discontinuity can be removed by defining g to be at that value. O B. g(x) has one discontinuity, and it can be removed by defining g to at that value. O C. g(x) has one discontinuity, and it cannot be removed. O D. g(x) has two discontinuities. The lesser discontinuity can be removed by defining g to be at that value. The greater discontinuity cannot be removed. O E. g(x) has two discontinuities. The lesser discontinuity cannot be removed. The greater discontinuity can be removed by setting g to be at that value. O F. g(x) has two discontinuities and neither can be removed