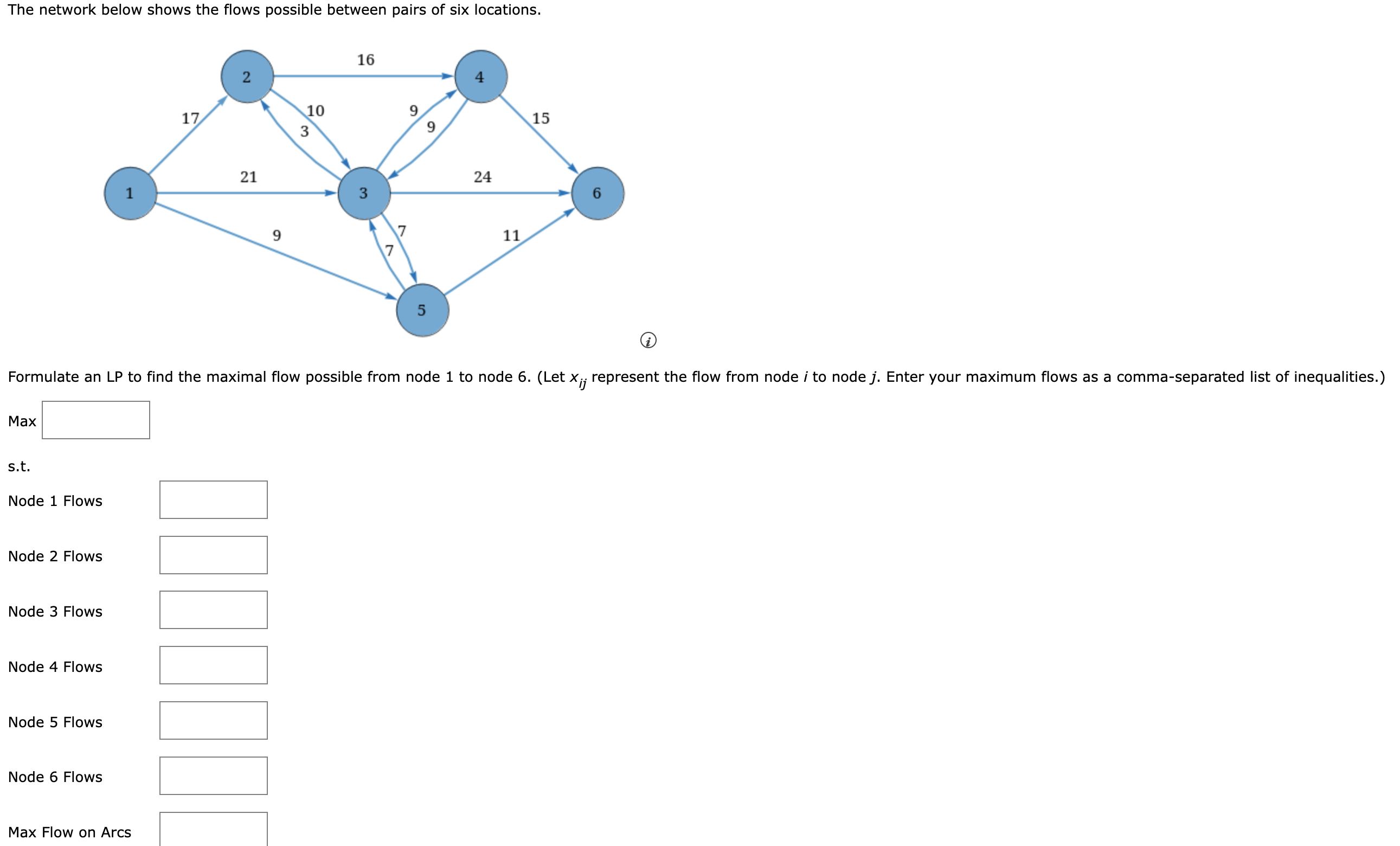
A graph with 6 nodes and 13 directed arcs is shown.

• Node 1 is connected to node 2 by arc of value 17, to node 3 by arc of value 21, and to node 5 by arc of value 9.
• Node 2 is connected to node 3 by arc of value 10 and to node 4 by arc of value 16.
• Node 3 is connected to node 2 by arc of value 3, to node 4 by arc of value 9, to node 5 by arc of value 7, and to node 6 by arc of value 24.
• Node 4 is connected to node 3 by arc of value 9 and to node 6 by arc of value 15.
• Node 5 is connected to node 3 by arc of value 7 and to node 6 by arc of value 11.
• Node 6 has no directed arcs directed to other nodes.

Formulate an LP to find the maximal flow possible from node 1 to node 6. (Let x_ij represent the flow from node i to node j. Enter your maximum flows as a comma-separated list of inequalities.)

Max_____

s.t.

Node 1 Flows _____

Node 2 Flows _____

Node 3 Flows _____

Node 4 Flows _____

Node 5 Flows _____

Node 6 Flows _____

Max Flow on Arcs _____

all x_ij 0 for all i and j.

Help, I will upvote

The network below shows the flows possible between pairs of six locations. Max s.t. Node 1 Flows Node 2 Flows Node 3 Flows Node 4 Flows Node 5 Flows Node 6 Flows Max Flow on Arcs