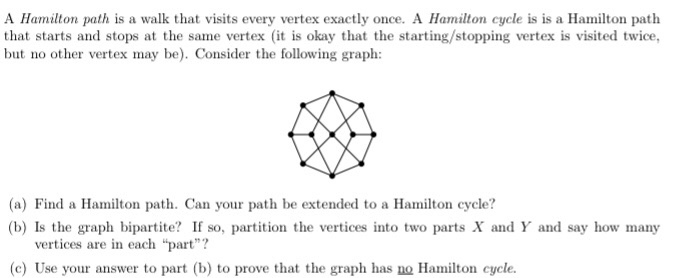
A Hamilton path is a walk that visits every vertex exactly once. A Hamilton cycle is is a Hamilton path that starts and stops at the same vertex it is okay that the starting/stopping vertex is visited twice but no other vertex may be). Consider the following graph: (a) Find a Hamilton path. Can your path be extended to a Hamilton cycle? (b) Is the graph bipartite? If so, partition the vertices into two parts X and Y and say how many vertices are in each "part"? (c) Use your answer to part (b) to prove that the graph has no Hamilton cycle